1.5.2. Графо-аналитический способ
Точность положения конечного пункта полигона по отношению к исходным пунктам наиболее полно характеризуется эллипсом ошибок.
Такой эллипс, построенный с использованием средних квадратических ошибок, называется средним эллипсом ошибок. Эллипс - геометрическое место точек с одинаковой плотностью вероятности. Имея средний эллипс ошибок, построенный в выбранном масштабе, можно получить среднюю квадратическую ошибку положения определяемого пункта по любому направлению. Ошибка положения пункта по данному направлению будет равна расстоянию от цента эллипса до подеры (педальной кривой, эвольвенты, кривой точности, кривой средних ошибок) по соответствующему направлению М.
Подера – это геометрическое место точек пересечения направлений, проведенных через центр, с перпендикулярами к этим направлениям, касательным к эллипсу.
Ошибка абсциссы (ординаты) определяемого пункта Мх (Му), соответствующая ошибке положения пункта по направлению, параллельному оси абсцисс (ординат), численно будет равна расстоянию от центра эллипса до подеры. Следовательно, имея, подеру (кривую точности) конечного пункта полигона, можно определить ошибку положения его в любом необходимом направлении.
Уравнение подеры записывается в виде:
где Рβ – радиус-вектор подеры (кривой точности);
А, В – большая и малая полуоси подеры;
Θ1 – дирекционный угол большой полуоси.
При графическом определении ошибок конечного пункта строят подеру от каждого источника: от ошибок при измерении горизонтальных углов Мβ; от случайных и систематических ошибок при измерении длин линий Мlμ, Mlλ; от ошибок при определении дирекционного угла исходной стороны МL0; по элементам найденных подер строят результирующую подеру (кривую точности).
Данные для создания таблицы представлены на схеме свободного висячего полигона
Построение подеры в зависимости от ошибок измерения углов.
Таблица 1.10
величина угла |
ср. ош. Измер угла |
Ri |
R/206 |
a=(R/206)*m𝛽 |
γi |
2γi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
216 |
20 |
2259,342 |
10,968 |
4387,072 |
307 |
254 |
136 |
20 |
2232,960 |
10,840 |
4335,845 |
308 |
256 |
180 |
20 |
2173,036 |
10,549 |
4219,487 |
308 |
256 |
214 |
20 |
2113,120 |
10,258 |
4103,146 |
308 |
256 |
221 |
20 |
2107,900 |
10,233 |
4093,010 |
308 |
256 |
189 |
20 |
2105,820 |
10,222 |
4088,971 |
308 |
256 |
180 |
20 |
2097,420 |
10,182 |
4072,660 |
310 |
260 |
180 |
20 |
2090,720 |
10,149 |
4059,650 |
310 |
260 |
180 |
20 |
2085,720 |
10,125 |
4049,942 |
310 |
260 |
141 |
20 |
2083,660 |
10,115 |
4045,942 |
310 |
260 |
132 |
20 |
2072,180 |
10,059 |
4023,650 |
314 |
268 |
180 |
20 |
2012,180 |
9,768 |
3907,146 |
314 |
268 |
180 |
20 |
1952,180 |
9,477 |
3790,641 |
314 |
268 |
180 |
20 |
1892,180 |
9,185 |
3674,136 |
314 |
268 |
180 |
20 |
1832,180 |
8,894 |
3557,631 |
314 |
268 |
180 |
20 |
1772,180 |
8,603 |
3441,126 |
314 |
268 |
180 |
20 |
1712,180 |
8,312 |
3324,621 |
314 |
268 |
180 |
20 |
1652,180 |
8,020 |
3208,117 |
314 |
268 |
180 |
20 |
1592,180 |
7,729 |
3091,612 |
314 |
268 |
180 |
20 |
1532,180 |
7,438 |
2975,107 |
314 |
268 |
180 |
20 |
1472,180 |
7,147 |
2858,602 |
314 |
268 |
180 |
20 |
1412,180 |
6,855 |
2742,097 |
314 |
268 |
180 |
20 |
1352,180 |
6,564 |
2625,592 |
314 |
268 |
180 |
20 |
1292,180 |
6,273 |
2509,087 |
314 |
268 |
180 |
20 |
1232,180 |
5,981 |
2392,583 |
314 |
268 |
180 |
20 |
1172,180 |
5,690 |
2276,078 |
314 |
268 |
180 |
20 |
1112,180 |
5,399 |
2159,573 |
314 |
268 |
180 |
20 |
1052,180 |
5,108 |
2043,068 |
314 |
268 |
180 |
20 |
992,180 |
4,816 |
1926,563 |
314 |
268 |
180 |
20 |
932,180 |
4,525 |
1810,058 |
314 |
268 |
180 |
20 |
872,180 |
4,234 |
1693,553 |
314 |
268 |
180 |
20 |
812,180 |
3,943 |
1577,049 |
314 |
268 |
180 |
20 |
752,180 |
3,651 |
1460,544 |
314 |
268 |
180 |
20 |
692,180 |
3,360 |
1344,039 |
314 |
268 |
180 |
20 |
632,180 |
3,069 |
1227,534 |
314 |
268 |
180 |
20 |
572,180 |
2,778 |
1111,029 |
314 |
268 |
180 |
20 |
512,180 |
2,486 |
994,524 |
314 |
268 |
180 |
20 |
452,180 |
2,195 |
878,019 |
314 |
268 |
180 |
20 |
392,180 |
1,904 |
761,515 |
314 |
268 |
180 |
20 |
332,180 |
1,613 |
645,010 |
314 |
268 |
180 |
20 |
272,180 |
1,321 |
528,505 |
314 |
268 |
180 |
20 |
212,180 |
1,030 |
412,000 |
314 |
268 |
180 |
20 |
152,180 |
0,739 |
295,495 |
314 |
268 |
180 |
20 |
92,180 |
0,447 |
178,990 |
314 |
268 |
180 |
20 |
32,180 |
0,156 |
62,485 |
314 |
268 |
|
|
|
|
|
|
|
|
|
|
Mб |
112963,103 |
|
|
Aβ2=1/2*(M β2+W β)
B β2=1/2*(M β2-W β)
W β- поправка к определению размеров полуосей подеры.
Для определения W β строим квадратичный полигон в удобном для построении масштабе по величине а и углу 2γi.
С квадратичного полигона на начальной его точке снимаем величину дирекционного угла 2θ2 направления W β, которое является удвоенным дирекционным углом малой полуоси. (рис 1.5)
(Рис 1.5) Квадратичный полигон для определения Wβ
Aβ2=1/2*(112963+41617.52)=278,011
B β2=1/2*(112963-41617.52)=188,87
2θ2=264
К определению радиус-векторов подеры
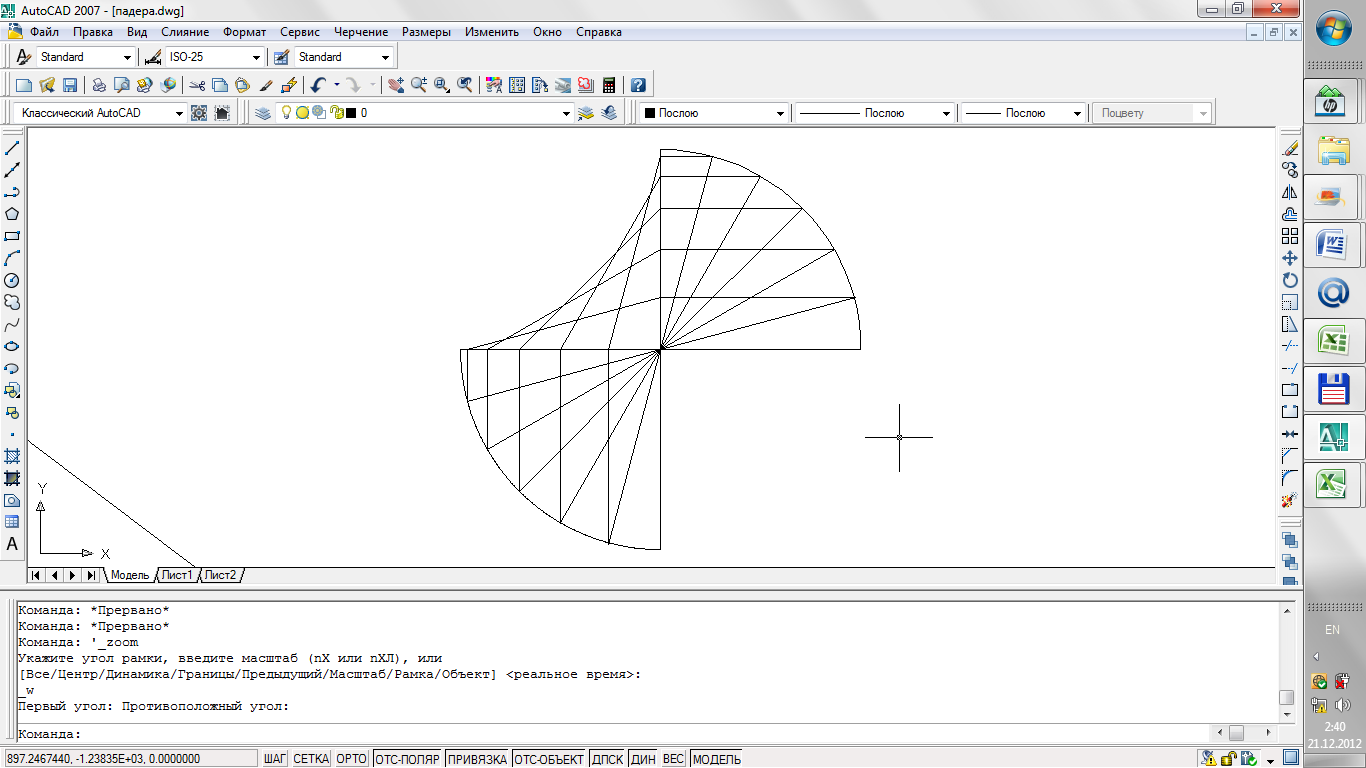
(рис 1.6) Схема к определению радиус-векторов подеры
По данному рисунку были сняты следующие данные для построения большой и малой полуоси
Таблица 2
φ |
Pβ |
15 |
1998,03 |
30 |
1997,46 |
45 |
1996,66 |
60 |
1995,93 |
75 |
1995,8 |