8. Индуктивность в цепи синусоидального тока.

Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции

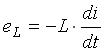(6.9)

Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = e_L = 0.

(6.10)

Таким образом, ток в индуктивности отстает по фазе от напряжения на 90^o из-за явления самоиндукции.       Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:

(6.11)

Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0^o< φ < 90^o), величина которого зависит от соотношения R и L.      Выражение (6.11) в комплексной форме записи имеет вид:

(6.12)

где Z_L - полное комплексное сопротивление индуктивной катушки

 Z_L - модуль комплексного сопротивления;

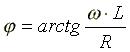- начальная фаза комплексного сопротивления;

- индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).        Полное сопротивление индуктивной катушки или модуль комплексного сопротивления

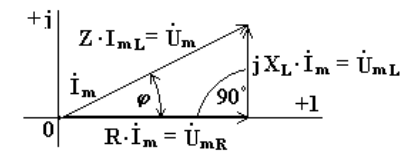
 Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).

(6.5)

 Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90^o.      В цепи  переменного тока напряжения на  участках цепи складываются не арифметически, а геометрически.         Если мы поделим стороны треугольника напряжений на величину тока I_m, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).

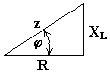(6.6) Из треугольника сопротивлений получим несколько формул:

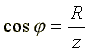
8. Емкость в цепи синусоидального тока

Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

(6,13)

Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90^o.

      Выражение (6.13) в комплексной форме записи имеет вид:

(6.14)

 где - емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

        Если комплексное сопротивление индуктивности положительно

, то комплексное сопротивление емкости отрицательно

На рис. 6.7 изображена векторная диаграмма цепи с емкостью.         Вектор тока опережает вектор напряжения на 90^o

(6.7)

8. Символический метод расчета цепей переменного тока.

http://www.websor.ru/metod_rascheta.html

Соединим последовательно лампу накаливания с сопротивлением R, батарею конденсаторов с емкостью С и катушку с большой индуктивностью L. Если данную цепь присоединить к зажимам генератора переменного тока, то лампа загорится, что свидетельствует о наличии электрического тока в цепи, несмотря на разрыв, существующий между изолированными друг от друга обкладками конденсатора. Для цепи переменного тока с последовательным соединением R, L, С (см. рисунок) дифференциальные уравнения по второму закону Кирхгофа имеют вид:

Здесь ток во всех трех участках один и тот же:

Разности потенциалов на всех трех сопротивлениях имеют вид:

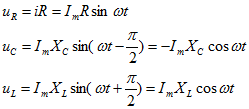
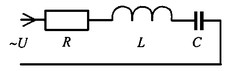
Решение системы дифференциальных уравнений можно существенно упростить, если перейти от дифференциальных уравнений к алгебраическим. Это можно сделать, изображая синусоидальные величины (i, u) в комплексной форме, т.е. в виде вектора на комплексной плоскости.

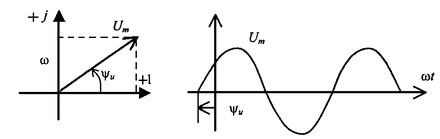Вектор Um и его проекции.

Расположим под углом   относительно оси абсцисс вектор Um, длина которого в масштабе равна амплитуде изображаемой величины. Положительные углы будем откладывать в направлении против часовой стрелки. Проекции вектора на вертикальную ось мнимых величин в комплексной плоскости равны мгновенному значению напряжения. Система векторов на комплексной плоскости называется векторной диаграммой. Вектора вращаются относительно центра координат с одной и той же скоростью и поэтому относительно друг друга их положение не меняется. Векторная диаграмма изображается неподвижной в заданный момент времени, определяемый начальнойфазой какой-либо величины, например, для идеальных элементов R, L, С

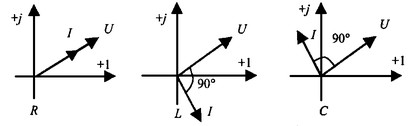Векторные диаграммы для идеальных элементов R, L, C.

Сложение двух функций в тригонометрической форме трудоемко, но легко производится в векторной форме.

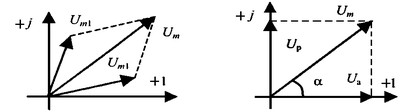Векторные диаграммы сложения двух напряжений

В расчетах применяют три формы записи комплексных величин: 

1) алгебраическая

2) тригонометрическая

3) показательная, учитывая

Символ j перед мнимой частью комплексного числа в алгебраической форме означает, что мнимая часть повернута по отношению к вещественной на угол 90° в положительном направлении (против часовой стрелки).  Переходы из одной формы записи в другие:

Где

Где

Представленная ранее система дифференциальных уравнений для цепи переменного тока с R, L, С в комплексном виде записывается следующим образом:

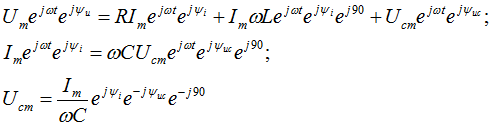
Используя выражения  , запишем выражение для полного напряжения цепи:

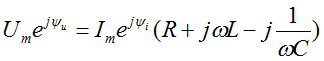
Где  - комплексное сопротивление; 

 - комплексная амплитуда напряжения; 

- комплексная амплитуда тока.  При замене амплитудных значений на действующие получим закон Ома в комплексной форме:

Величину Z называют полным сопротивлением цепи переменного тока.  Первый закон Кирхгофа в комплексной форме:

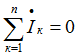
Второй закон Кирхгофа в комплексной форме:

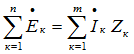
Векторная диаграмма напряжений для цепи с последовательным соединением R, L, C будет представлять собой прямоугольный треугольник.

Треугольник напряжений

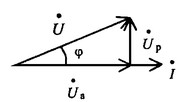
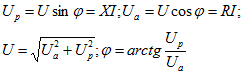
Треугольники токов, сопротивлений и мощностей строятся аналогично

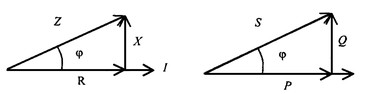
Полная мощность S = UI; активная мощность    реактивная мощность где

 

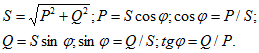
В треугольниках напряжений, токов, сопротивлений и мощностей угол  сохраняет свое значение.  При параллельном соединении ветвей их проводимости складываются в комплексной форме:

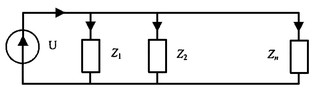
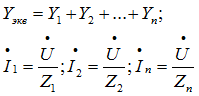Общий ток, согласно первому закону Кирхгофа:

8. Мощности в цепи синусоидального тока. Треугольник мощностей.

http://toe-kgeu.ru/toe1/286-toe1

8. Понятие о трехфазных системах. Трехфазный синхронный генератор.

8. Способы соединения трехфазных цепей.

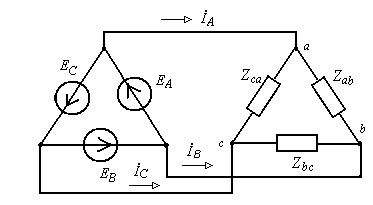
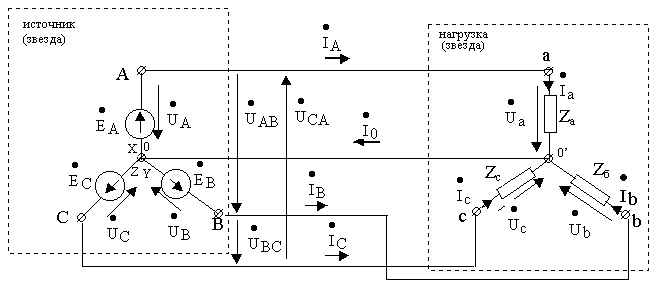
8. Определения линейных и фазных величин в трёхфазных цепях.

9. Основные понятия магнитных цепей.

http://toe-kgeu.ru/toe3/393-toe3