23.Определение устойчивости по логарифмическим характеристикам

Для устойчивости замкнутой системы необходимо и достаточно, чтобы ЛАЧХ разомкнутой системы пересекала ось частот раньше чем ЛФЧХ линию фазового сдвига –π.

Для устойчивости необходимо и достаточно, чтобы частота среза располагалась левее точки пересечения ЛФЧХ с линией фазового сдвига –π.

Для устойчивости замкнутой системы необходимо и достаточно, чтобы при положительных значениях ЛАЧХ разность между числом положительных(снизу вверх) и отрицательных(с верху вниз) переходов фазочастотной характеристики линии фазового сдвига –π=l/2, где l – число правых корней характеристического уравнения разомкнутой системы. Начало характеристики на линии фазового сдвига принимается за 0,5 перехода.

Логарифмический критерий устойчивости позволяет просто определить запасы устойчивости системы по амплитуде.

h1, h2– запас устойчивости системы по амплитуде.

Φ – запас устойчивости системы по фазе.

Необходимые значения запаса устойчивости зависят от классов систем и требований к качеству регулирования.

Ориентировочно: Δφ(w)=30..60⁰; Δl(w)=6..20 дб.

24.Запасы устойчивости

∆А =1-│А(кр)│, =180-│(ср)│

∆L =L(кр); =180-│(ср)│

Устой-ть лин.сис.опред-ся ее хар.ур.коэф-ы хар.ур.парам-ы к-го зависят только от св-в сис-ы малейшее изменение парам-в м-т привести к потери уст-ти,т.е.измен-е технич-х св-в сис-ы.Д/этого при проектир-ие технич-х сис.вводят понятие запасов устойчивости: 1.запас устой-ти по модулю.2.- .-.-по фазе.1.∆А показ-ет на сколько АФЧХ разом-ой сис.отличается от единицы.2.по фазе,показ-т насколько фаза отлич-я от 180 при единич-й амплитуде. В логариф-ом масшт-е запас устой-ти по амплитуде ∆L-это вел-на ЛАХ в критич-й частоте.

25.Точность сау. Основные понятия.

Выделяют статич-е и астатич-е сис. ДУ ошибки возникающ-е в сис.регулиров-я получают из передаточ-й ф-и ошибки обратным преобраз-ем Лапласа Учитывая приведен.ф-ы изобр-е ошибки в сис.опред-я как E(P)=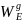 (P)G(P) исполь-я обрат-е преоб-я Лапласа и расклад-я передаточ.ф-ю ошибки в рад Тейлора получим

, С_i-коэф.ошибк,C₀-коэф.ош.по положению, C₁-коэф.ош.по скорости измен-я вх.сиг-а, C₂-коэф.ошибки по ускорению измен.вх.сиг-а.

На практике исполь-т первые 3 коэф-а. остальные коэф. го влияния не оказыв-т,т.к.очень малы.

Для того чтобы импульсная система имела нулевую установившуюся ошибку по задающему воздействию, необходимо, чтобы порядок ее астатизма по задающему воздействию превышал степень входного воздействия. Аналогично определяется и астатизм по возмущающему воздействию.

26.Статические и астатические сау.

Д/сис-ы разомк-я передаточ-я сис.им.вид астатизм опр-ся кол-м интегрир-х звеньев. Если сис.стат-я,то коэф.=0,т.е.интегр-е звенья отсут-т. Если g(t)=1(t); (t)=C₀,при этом , k-общ.коэф.усиления сис. k = b₀/α₀ Если g(t)=at, E(t)=C₀at+C₂a. Если g(t)=at²/2, E(t)=C₀(Ut²)/2+C1at+C2a. В стат.сис.все Сi≠0. Если астатизм 1го порядка =1,то g(t)=1(t),E(t)=0, тк С0=0; g(t)=at,E(t)=C1a, C1=1/k; g(t)=at²/2, E(t)=C1at+C2a Если =2, С0=0, С1=0,С2≠0 тогда g(t)=1(t) и g(t)=at, E(t)=0; g(t)=at2/2,E(t)=C2a,C2=1/k.

 сис.в к-х ошибка регулир-я =0; но при этом должно соблюд-ся усл-ие, степень передав-го сиг-ла д/б на един-у меньше чем степень астатизма сис.,нулевая ошибка при х воздей-х приводит сис.к инвариантности,выделяют полную и частичную инвариантности.