
- •Основные понятия и определения тау.
- •2.Принципы управления.
- •3. Классификация сау.
- •4.Системы автоматической стабилизации, программного управления и следящие сау.
- •Системы автоматический стабилизации
- •Системы программного регулирования
- •Следящие системы
- •5.Типовая структура сау.
- •6.Математическое описание сау. Дифференциальные уравнения.
- •7.Математическое описание сау. Преобразование Лапласа. Понятие передаточной функции системы.
- •8.Математическое описание сау. Частотные характеристики сау.
- •9.Математическое описание сау. Логарифмические частотные характеристики.
- •10.Математическое описание сау. Временные характеристики.
- •11.Типовые динамические звенья. Интегрирующее звено.
- •18.Построение логарифмических характеристик последовательно соединенных звеньев.
- •19.Устойчивость сау. Понятие устойчивости.
- •20.Критерии устойчивости. Критерий Гурвица.
- •21.Критерии устойчивости. Критерий Найквиста.
- •22.Критерии устойчивости. Критерий Михайлова.
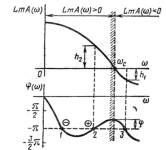
- •23.Определение устойчивости по логарифмическим характеристикам
- •24.Запасы устойчивости
- •25.Точность сау. Основные понятия.
- •26.Статические и астатические сау.
- •27.Качество регулирования. Основные показатели качества регулирования.
- •28.Коррекция сау
- •29.Построение желаемой логарифмической характеристики Построение желаемых логарифмических амплитудно-частотных и фазочастотных характеристик
- •30.Нелинейные сау. Основные отличия нелинейных систем от линейных.
- •31.Основные типовые нелинейности
- •32.Правила преобразования структурных схем нелинейных сау
- •33.Абсолютная устойчивость. Критерий устойчивости Попова
- •34.Метод гармонического баланса
- •35.Понятие автоколебаний. Устойчивость автоколебаний.
- •36.Дискретные сау. Основные понятия. Квантование.
- •37.Импульсные сау. Понятие модуляции.
- •38.Математическое описание исау. Z-преобразование. Дискретное преобразование Лапласа.
- •Системы автоматический стабилизации
- •Системы программного регулирования
- •Следящие системы
8.Математическое описание сау. Частотные характеристики сау.
Если
на вх-ю сис.под-ся гармонич-е возде-е
вид g(t)=Aвхsint,
то на вых-й-x(t)=Aвыхsin(t+)
но с др.амплитудой и частотой.
А-амплитуда,-отстование
по фазе. В дан.случ-е отнош-е вых. И вх.
сиг-а опре-т амплитудно-фазную частот-ю
хар-ку сис-у (АФЧХ). АФЧХ также м-о получ-ь
из перед-й ф-и сис-ы. Д/этого оператора
Лапласа p=j,
j= ,
тогда АФЧХ соотв-и ф-и (1) буд.им.вид
,
тогда АФЧХ соотв-и ф-и (1) буд.им.вид
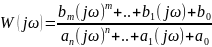 (2) т.к. АФЧХ хар-т изм-е сиг-а на вых. И
явл.комплек-й вел-й, то (2) м-о пред-ь 1)
(2) т.к. АФЧХ хар-т изм-е сиг-а на вых. И
явл.комплек-й вел-й, то (2) м-о пред-ь 1)
 ,
2)
,
2) .
Кажд.из испл-х хар-к исп-т д/анализа
синтеза САУ. А()
– АЧХ, ()-
ФЧХ, Re()-веществе-я
частот-я хар-а, Im()
– мнимая чх. АФЧХ сис.строят на комплексной
пл-ти при измен-и частоты от 0 до .
.
Кажд.из испл-х хар-к исп-т д/анализа
синтеза САУ. А()
– АЧХ, ()-
ФЧХ, Re()-веществе-я
частот-я хар-а, Im()
– мнимая чх. АФЧХ сис.строят на комплексной
пл-ти при измен-и частоты от 0 до .
![]() =(0,).
A()=
=(0,).
A()= , ()=arctg
, ()=arctg
9.Математическое описание сау. Логарифмические частотные характеристики.
При анализе Сау часто исп.логарифм.хар-и. Выделим 2 типа: логарифм-амплитудная (ЛАХ) L()=20lgA(W), лог-ая-фазовая (ЛФХ). При постр.графика лх по оси ординат откладывают усиление(амплитуду) к-я изм-я в децибелах,по оси абсцисс л.частоты.
![]() При
постр. ФХ откладыв. ()
град.раб.
При
постр. ФХ откладыв. ()
град.раб.
10.Математическое описание сау. Временные характеристики.
При
исследов.поведения САУ часто рассм.реакцию
сис.на типовые управляющие сигналы к
типовым сиг-м отн.единично-ступенчатое,воздействие
в виде β-ф-и, гармонич.возд.,возд.в виде
полинома. Если на ход сис.подают
единичн.ступенчатые возд. g(t)=1(t)= то
вых.сиг-л наз.переходной ф-ей сис-ы
кот.явл.одной из осн.хар-к. Переходн.ф-цией
сист.наз.переходный проц.вызван.единичным
ступенчатым воздействием при нулевых
нач.усл-х. Переходн.проц.чич.получ.исп.обр.преобраз.Лапласа.
x(t)=
то
вых.сиг-л наз.переходной ф-ей сис-ы
кот.явл.одной из осн.хар-к. Переходн.ф-цией
сист.наз.переходный проц.вызван.единичным
ступенчатым воздействием при нулевых
нач.усл-х. Переходн.проц.чич.получ.исп.обр.преобраз.Лапласа.
x(t)=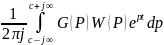 ,
1(t)=1/p,
т.к.изобр.единичн.возд.1/p,
то перех.ф-я выдел.выр-ем: h(t)=
,
1(t)=1/p,
т.к.изобр.единичн.возд.1/p,
то перех.ф-я выдел.выр-ем: h(t)=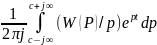
![]() Р-ция
сис.на типовое возд.в виде ∆ ф-и
наз.весовой хар.сис.или импульсной
перех.ф-й. Осн.св-во:достич.max
знач.в опр.мом.вр. g(t)=(t)=
Р-ция
сис.на типовое возд.в виде ∆ ф-и
наз.весовой хар.сис.или импульсной
перех.ф-й. Осн.св-во:достич.max
знач.в опр.мом.вр. g(t)=(t)= .
.
Изображ.по
Лапласу ∆ ф-и=1: (t)=1.
Примем обр.преобр.Лапласа получ.лин.перед.ф-я.
ku(t)=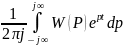
![]()
11.Типовые динамические звенья. Интегрирующее звено.
Пусть
САУ описыв ЛДУ вида
 Числитель и знаменатель явл.полиномами
кот.им.нулевые, вещественные и
комплексно-сопряженные. В итоге
передат.ф-ю сис.м-о предст-ть как
произведение типовых звеньев W(P)=k
Числитель и знаменатель явл.полиномами
кот.им.нулевые, вещественные и
комплексно-сопряженные. В итоге
передат.ф-ю сис.м-о предст-ть как
произведение типовых звеньев W(P)=k
Идеальное-инерционное (интегрирующее) W(P)=k/p, k-коэф-т усиления сис-мы
Так называют звено с передаточной функцией W(s) = к/s. Его частотные и временные функции имеют следующий вид:
![]()
АФЧХ:
![]()
ЛАХ, ЛФХ:
![]()
Переходная характеристика:
![]()
k-коэфф усиления
12.Типовые динамические звенья. Апериодическое звено.
Инерционное 1 пор.Так называют звено с передаточной функцией W(s) = k/(Ts + 1). Его частотные и временные функции имеют следующий вид:
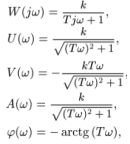
![]()
АФЧХ:
![]()
ЛАХ, ЛФХ:
![]()
Переходная характеристика:
![]()
13.Типовые динамические звенья. Колебательное звено.
Инерционное 2 пор. Так называют звено с передаточной функцией:
![]()
АФЧХ:
![]()
ЛАХ,ЛФХ:
![]()
Переходная характеристика:
![]()
14.Типовые динамические звенья. Идеальное дифференцирующее звено.
Дифференцирующее звено. Так называют звено с передаточной функцией W(s) = ks. Его частотные и временные функции имеют следующий вид:
![]()
АФЧХ:
![]()
ЛАХ, ЛФХ:
![]()
15.Типовые динамические звенья. Дифференцирующее звено первого порядка.
Передаточная функция:
W(p)=k(τp+1)
![]()
h(t)=k[τ(t)+1(t)] x=1(t)
![]()
![]()
![]()
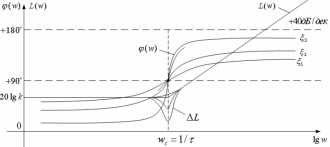
16.Типовые динамические звенья. Дифференцирующее звено второго порядка.
Передаточная функция:
W(p)=k(τ2p2+2ξτp+1)
![]()
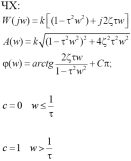
![]()
![]()
![]()
![]()
17.Преобразование структурных схем.
Существует 3 осн вида соединения звеньев:
-последовательное
-параллельное
-обратной связи
1) Так называется соединение, при котором выходная переменная предшествующего звена является входной переменной последующего звена
![]()
При последовательном соединении передаточные функции отдельных звеньев перемножаются, и при преобразовании структурных схем цепочку из
п![]() оследовательно
соединенных звеньев можно заменить
одним звеном с передаточной функцией
оследовательно
соединенных звеньев можно заменить
одним звеном с передаточной функцией
![]()
2)Так называется соединение, при котором на входы всех звеньев подается одно и то же воздействие, а их выходные переменные складываются
![]()
При параллельном соединении звеньев передаточные функции складываются, и при преобразовании их можно заменить одним звеном с передаточной функцией
![]()
Если выход какого-либо звена
поступает на сумматор с отрицательным знаком, то передаточная
функция этого звена складывается с отрицательным знаком, т.е. вычитается
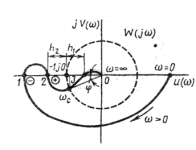
3) Обратное соединение, или звено, охваченное обратной связью. Так называется соединение двух звеньев, при котором выход звена прямой цепи подается на вход звена обратной связи, выход которого складывается с входом первого звена Если сигнал обратной связи вычитается, то обратная связь называется отрицательной, в противном случае — положительной.
![]()
![]()
![]()
Передаточная функция:
![]()
Перенос сумматора:
При переносе сумматора по ходу сигна-
сигнала добавляется звено с передаточной функцией, равной передаточной
функции звена, через которое переносится звено.
При переносе сумматора против хода сигнала добавляется звено с передаточной функцией, равной обратной передаточной функции звена,
через которое переносится сумматор.
![]()
![]()
Перенос узла. При переносе узла по ходу сигнала добавляется звено с передаточной функцией, равной обратной передаточной функции звена, через которое переносится узел
При переносе узла против хода сигнала добавляется звено с передаточной функцией, равной передаточной функции звена, через которое переносится
узел
![]()
