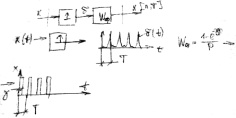
37.Импульсные сау. Понятие модуляции.

Импульсные системы – это такие САУ, в которых имеются сигналы квантованные по времени.

В завис-ти от вида квант-я выдел.3 вида дискрет-х сис.:1. Если ося кван-е сигн-ла по уровню,то это рылейная сис-а.2. если по вр-и то импульсные сис-ы. 3. Если по уровню и ппо вр-и то цифровая сис-ма.т.о.раб-а импул-х сис-м связана с воздей-ем и передачей послед-ти импульсов. В импульс-х сис. в отличии от непрерыв-х у к-х изменение сигнала происх-т в кажд.мом.вр.происход-т преобразов-е (дискритизация сигналов) последовательность импульсов. Дискритизация ося в 2 этапа:1 происх-т квантов-е сиг-ла по вр-ни 2.Модуляция-преобраз-е квантового сигнала в импульсную последовательность в соответ-ии с законами модуляции выдел-т 3 основ-х закона модуляции:1)амплитудно-импульсная модуляция 2)частотно-импул-я 3)широто-имп-ая. При 1) аи формирмир-ся импульсы след-ии с постоя-й частатой и широтой, но с переменной амплитудой. При 3) амплитуда и частота постоя-ы, широта разная. 2) амплитуда и широта пост-ы, частота-разная. импуль-й эл-т в нем квантование

38.Математическое описание исау. Z-преобразование. Дискретное преобразование Лапласа.

Эти преобразования позволяют распространить все методы линейных систем на импульсные системы.

• Квантованный сигнал, который рассматривается лишь в дискретные моменты времени f(kT), может быть подвергнут дискретному преобразованию Лапласа по следующей формуле: (4,1)

Обычно после вычисления получается дробно-рациональная функция

переменного е^р .

Другим способом преобразования квантованного сигнала является Z-преобразование: F(z) = Z{f(t)} = Z{f(kT)}

(4.2)

Нетрудно видеть, что имеется простая зависимость:

С ущественным преимуществом Z-преобразования является то, что все выражения являются дробно-рациональными функциями, такими же, как и в обычном преобразовании Лапласа. Дискретное преобразование Лапласа (также, как и Z-преобразование,) обладают всеми свойствами, относящимися к обычному преобразованию Лапласа. Имеется целый ряд теорем, аналогичных теоремам о дифференцировании и интегрировании оригинала обычного преобразования Лапласа. Только в дискретном случае вместо дифференцирования и интегрирования фигурируют сдвиги во времени.

Вычисление Z-преобразований

Способ 1 (по определению)

Пример: f(kT)=1(t). Это - единичная ступенчатая функция.

39. Математическое описание ИСАУ. Передаточная функция разомкнутой и замкнутой ИСАУ.

Передаточная функция импульсной системы

Пусть на входе импульсной системы имеется импульсный сигнал u(z), на выходе этой системы имеется соответствующий сигнал Y(z). при нулевых начальных условиях

Возникает стандартная задача вычисления импульсной передаточной функции для импульсной системы, если известен исходный непрерывный прототип.

Мы рассматриваем входной и выходной сигналы лишь в моменты квантования, а не как непрерывную функцию, поэтому на выходе системы имеется ещё один (фиктивный) квантователь. Сигнал Y(p) имеет сложную форму, совсем не похожую на квантованный сигнал. Основная формула для импульсной передаточной функции основывается на доказанной в предыдущей лекции формуле для спектра идеального квантователя.

Замечание:

По формуле (3.1) видно, что преобразования Лапласа идеального

квантованного сигнала является периодической функцией с периодом jωp.

Как следствие, из этого вытекает, что частотные характеристики импульсного сигнала и амплитудно-частотная, фазо-частотная являются периодичными с

периодом jω .

При то есть получаем импульсную передаточную функцию в терминах Z - преобразования, без фиксатора. Заметим, что из формулы (8) видно, что: результат квантования произведения не обязательно равен произведению результатов квантования.

Имеются обширные таблицы, в которых для стандартных и непрерывных передаточных функций имеются импульсные передаточные функции.

Передаточная функция замкнутой системы

В импульсной системе не всегда можно вычислить передаточную функцию замкнутой системы по подобной формуле. Сама эта возможность связана с наличием и расположением квантователя. Рассмотрим некоторые возможные случаи расположения квантователей в системе.

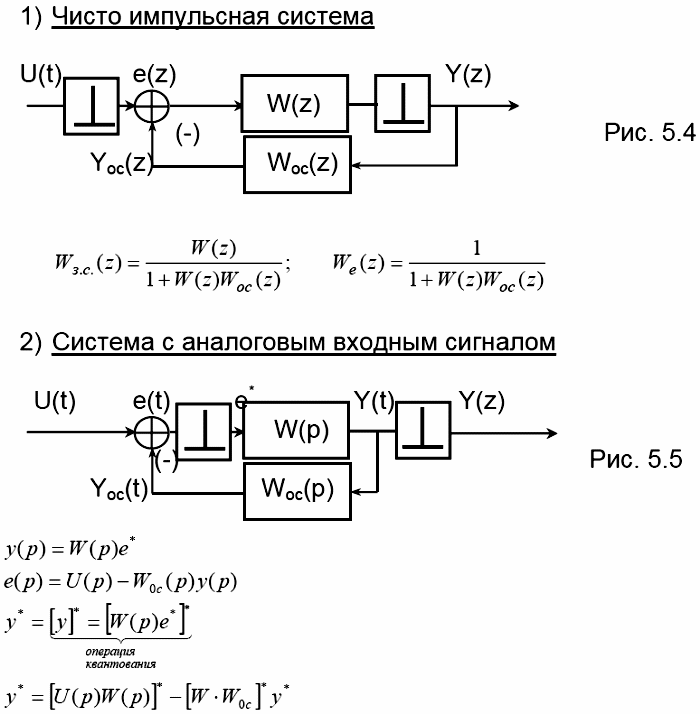
Раскрывать скобки нельзя, поэтому из последней формулы y* выразить через Wзс и U(p) нельзя. Результат квантования произведения не обязательно равен произведению результатов квантования. В этом случае не получается формулы для передаточной функции замкнутой системы ! Если, однако, два блока разделены квантователем, то результирующая импульсная передаточная функция равна произведению импульсных ПФ отдельных блоков. Для этого также имеет смысл включать в состав системы фиктивные квантователи.

Таким образом, в практически важном случае следящей системы вид импульсной передаточной функции замкнутой системы не отличается от обычного. То же справедливо и для ПФ по ошибке.

40.Устойчивость ИСАУ. Алгебраические критерии устойчивости.

41.Устойчивость ИСАУ. Частотные критерии устойчивости.

42.Устойчивость ИСАУ. Влияние на устойчивость ИСАУ квантования по времени.

43.Многомерные САУ.Математическое описание многомерных систем.

4.Системы автоматической стабилизации, программного управления и следящие САУ.

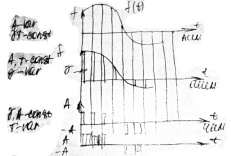
Системы автоматического регулирования в зависимости от характера изменения управляющего воздействия делятся на три касса. Различают системы автоматической стабилизации, системы программного регулирования и следящие системы.

Системы автоматической стабилизации характеризуются тем, что в процессе работы системы управляющее воздействие остаётся величиной постоянной.

 САУ в зависимости от характера изменения управляющего воздействия делятся на три класса:

 1) – системы автоматический стабилизации;

 2) – системы программного регулирования;

 3) – следящие системы.