34.Метод гармонического баланса

 нелин.сис.м-о представить в виде лин.эл-та с перед-й ф-й Wл и н.э. Одним из св-в нелин.сис.явл.возмож-ь возник-ия в дан-х сис-х переодич-го решения,т.е. сис.нах-я в автоколеб-ом режиме совер-т движ-е с постоян-й амплитудой и частотой. Если на вх.нелин.сис.податьгармонич-й сиг-л х=А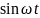 ,то лин. Часть явл.низкочастот-м фильтром и на вх.н.э.также будет поступать гармонич-е воздей-е т.о.вых.сиг-л нелин.сис.будет явл.ф-й y=F(x)=F(A ). Дан.ф-ю м-о разложить в ряд Ф-е и получить описание выхода н.э.такой метод наз.методом гармонич.баланса дан.метод исполь-ся д/линеаризации н.э.с целью упрощения поиска переодич-х реше-й. Разложим ф-ю F в ряд Ф-е и выделим 1ую гармонику. y=A0+A1 +B1 При нулевых нач.усл-х А0=0, А1= ; B1= , т.о.вх.сиг-л н.э.явл.зависимостью от амплитуды введем понятие эквивалентной передаточ-й ф-и н.э. 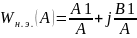. Нелинеариз-аю лин.сис.м-о пред-ть кривой на комплек-й пл-ти тогда н.сис.

35.Понятие автоколебаний. Устойчивость автоколебаний.

Автоколебания – собственные колебания в нелинейной системе, обладающие свойством устойчивости, т.е. способностью сохранять амплитуду и форму колебаний.

Т.к.методом гармонич.баланса была получ.нелин.сис.то она обладает св-ми лин-х сис-м,в лин-х сис-х атоколебания возникают,т.е.такая сис.наз.условно устойчивой

Передат-ая ф-я замк-й сис.вида Будет усл.уст-й если выпол-ся усл-ие на границе если W_A= введем понятие обратной хар-ки н.э. 1/Wнэ=z(A) условие Wл(j)=-z(A)

т .о.автоколеб-я возник-т в т-х W(j) пересеч-я с обрат-й не лин-й харак-и (-z(A))

Устойчивость автоколебания

Как видно из графика  2 т.пересечения харак-к, что свидет-ет о наличие автоколеб-й вида -неусто-й автоколеб.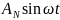 -уст.а/к. Устойч-и явл.а/к к-е возник-т в техническиреализ-х сис-х,т.е.в сис-х м-т наблюдаться только 1 решение (переодич.). Устой-ть переодич-го реш-я опред-ся по след-м правилам: если при движении по обратной нелин.харак-и –z(A) в сторону увел-я амплитуды т.пересеч-я характеристик явл.т.входа в линейную харак-ку,то в дан-й т.будет неустой-е переод-е решение. Если т-й пересеч-я явл.т-й выхода, то дан-й точки устойчи-й переодич.решение.

36.Дискретные сау. Основные понятия. Квантование.

Определение дискретной САУ.

Система автоматического управления называется дискретной, если выходная величина какого – либо ее элемента имеет дискретный характер.

Большое внимание к теории и практике дискретных систем объясняется все большим использованием в замкнутом контуре управления цифровых вычислительных машин (ЦВМ). Это обеспечивает системе значительно большие вычислительные возможности, высокую стабильность, простоту перестройки ее структуры и параметров.

Так как информация о состоянии объекта управления является непрерывной, то перед подачей на вход ЦВМ ее необходимо преобразовать в дискретную форму. Эту задачу выполняет преобразователь “ аналог – код ”, который в теории автоматического управления принято называть импульсным элементом” (ИЭ). Дискретизация осуществляется путем квантования непрерывного сигнала по времени и по уровню. Преобразование непрерывного сигнала в импульсный называетсяся квантованием.

Система с квантованием только по времени – импульсная. Система с квантованием и по времени и по уровню – дискретная.

С хема дискретной САУ

На схеме под W_нч(s) подразумевается непрерывная часть системы. Следует отметить, что так как в состав системы входят как дискретные, так ианалоговые элементы, то такие системы часто называют дискретно – непрерывными или гибридными.

1. Квантование по уровню – это преобразование сигнала с помощью АЦП/ЦАП, когда диапазон изменения сигнала делится на ступени в зависимости от разрядности АЦП/ЦАП. Сейчас в промышленных применениях в основном используются 14- 16-разрядные квантователи. Значительно реже 8 и 10- разрядные. 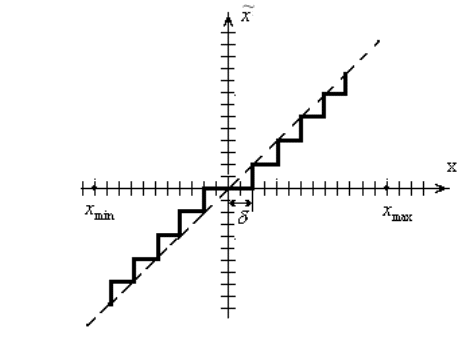Ступенчатая линия описывает преобразование непрерывной величины х(t) в квантованную по уровню величину (kT). где n – разрядность кода.

2. Квантование по времени возникает в системе из-за того, что ввод и вывод информации в ЭВМ происходит с некоторой периодичностью и не чаще. Пусть T – период квантования по времени. При правильном проектирование САУ (с достаточной разрядностью по АЦП/ЦАП) КПУ чаще всего можно пренебречь, если учесть накопление погрешности, а КПВ необходимо учитывать. Как правило, не удается сделать скорость ввод/вывод информации до такой степени высокой, чтобы полностью пренебречь квантованием по времени. Поэтому важно иметь теорию расчёта САУ с учётом КПВ. Системы, в которых имеется только квантование по времени (КПВ), а квантованием по уровню (КПУ) можно пренебречь, называются импульсными в отличие от дискретных систем. Дискретные системы – нелинейные, их изучение представляет сложную задачу, ее лучше избегать, повышая разрядность квантования. Для импульсных систем имеется удобный математический аппарат.