39. Уравнение адиабаты идеального газа.
Для
0%98%D0%B4%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B3%D0%B0%D0%B7"идеальных
газов,
чью теплоёмкость можно считать постоянной,
в случае
0%9A%D0%B2%D0%B0%D0%B7%D0%B8%D1%81%D1%82%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BF%D1%80%D0%BE%D1%86%D0%B5%D1%81%D1%81"квазистатического
процесса
адиабата имеет простейший вид и
определяется уравнением[
где:
V — его 0%9E%D0%B1%D1%8A%D1%91%D0%BC"объём,
—
0%9F%D0%BE%D0%BA%D0%B0%D0%B7%D0%B0%D1%82%D0%B5%D0%BB%D1%8C_%D0%B0%D0%B4%D0%B8%D0%B0%D0%B1%D0%B0%D1%82%D1%8B"показатель
адиабаты,
и
—
0%A2%D0%B5%D0%BF%D0%BB%D0%BE%D1%91%D0%BC%D0%BA%D0%BE%D1%81%D1%82%D1%8C"теплоёмкости
газа соответственно при постоянном
давлении и постоянном объёме.
С учётом 0%A3%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D1%81%D0%BE%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%B8%D1%8F_%D0%B8%D0%B4%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE_%D0%B3%D0%B0%D0%B7%D0%B0"уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду:
,
где T — 0%90%D0%B1%D1%81%D0%BE%D0%BB%D1%8E%D1%82%D0%BD%D0%B0%D1%8F_%D1%82%D0%B5%D0%BC%D0%BF%D0%B5%D1%80%D0%B0%D1%82%D1%83%D1%80%D0%B0"абсолютная температура газа. Или к виду:
Поскольку Kвсегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении V) газ нагревается (T возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент K.
40. Политропические процессы.
Политропический
процесс, политропный
процесс, изменение состояния физической
системы, при котором сохраняется
постоянной её
0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%91%D0%A1%D0%AD/%D0%A2%D0%B5%D0%BF%D0%BB%D0%BE%D1%91%D0%BC%D0%BA%D0%BE%D1%81%D1%82%D1%8C/"теплоёмкость
(С).
Кривая на термодинамических диаграммах,
изображающая П. п., называется
0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%91%D0%A1%D0%AD/%D0%9F%D0%BE%D0%BB%D0%B8%D1%82%D1%80%D0%BE%D0%BF%D0%B0/"политропой.
Простейшим примером обратимого П. п.
может служить П. п. с
0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%91%D0%A1%D0%AD/%D0%98%D0%B4%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9%20%D0%B3%D0%B0%D0%B7/"идеальным
газом,
определяемый уравнением pVn
=const,
где р
— давление, V
—
объем газа,
показатель
политропы (Cp
и Cv
— теплоёмкости
газа соответственно при постоянном
давлении и объёме). Используя
0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%91%D0%A1%D0%AD/%D0%A3%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5%20%D1%81%D0%BE%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%B8%D1%8F/"уравнение
состояния
идеального газа, уравнение политропы
можно записать в ином виде:
const
или
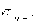const
(здесь Т
— абсолютная
температура).уравнение П. п. идеального
газа включает, как частные случаи,
уравнения:
0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%91%D0%A1%D0%AD/%D0%90%D0%B4%D0%B8%D0%B0%D0%B1%D0%B0%D1%82%D0%B0/"адиабаты
(С =0,
n =Cp/Cv,
это отношение теплоёмкостей обозначают
g),
0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%91%D0%A1%D0%AD/%D0%98%D0%B7%D0%BE%D0%B1%D0%B0%D1%80%D0%B0/"изобары
(С =
Ср,
n =
0),
0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%91%D0%A1%D0%AD/%D0%98%D0%B7%D0%BE%D1%85%D0%BE%D1%80%D0%B0/"изохоры
(С = Cv,
n =
¥) и
0%BA%D0%BD%D0%B8%D0%B3%D0%B8/%D0%91%D0%A1%D0%AD/%D0%98%D0%B7%D0%BE%D1%82%D0%B5%D1%80%D0%BC%D1%8B/"изотермы
(С = ¥, n
=
1). РаботаАидеального
газа в П. п. против внешнего давления
определяется по формуле
,
где индексами 1 и 2 обозначены начальное
и конечное состояния газа. Понятием П.
п. широко пользуются в технической
термодинамике при исследовании рабочих
циклов тепловых двигателей.