23. Производная функции, заданной параметрически. Производная вектор-функции.

.Предположим ,что дифф-мы любое кол-во раз по переменной t.Кроме того будем считать,что k= имеет в окрестности данной фиксированной точки tобратную ф-цию:

t= ^-1(x)

y=Ψ( ^-1(x))

y=y(x)

Тогда:dy/dx= Ψ’( ^-1(x))* ( ^-1(x))’

dy/dx= / .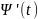

24. Основные теоремы о дифференцируемых функциях.

Теорема1 (Ферма) Пусть функция f(x) имеет на множестве E точку экстремума x₀€E, причём множество E содержит некоторую -окрестность 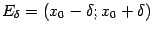точки x₀ . Тогда либо f(x) имеет в точке x₀ производную, равную 0, то есть , либо производная в точке x₀ не существует.

Поведение функции в окрестности точки экстремума

Замечание: Заметим, что условие означает, что тангенс угла наклона касательной к графику y=f(x) , проведённой при x=x₀, равен 0. Отсюда α=0, то есть теорема Ферма утверждает, что касательная, проведённая в точке экстремума, горизонтальна (если эта касательная существует).

Теорема2 (Ролля) Пусть функция f(x) дифференцируема на интервале (a;b), непрерывна в точках a и b и принимает в этих точках значение 0: . Тогда найдётся хотя бы одна точка 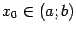, в которой .

Заметим также, что теорема Ролля не утверждает, что корень x₀-- единственный корень производной на интервале (a;b); на этом интервале может находиться несколько корней производной.

Рис. Между двумя корнями дифференцируемой функции лежит хотя бы один корень её производной/.

Теорема3 (Лагранжа) : Пусть функция f(x) дифференцируема на интервале (a;b) и непрерывна в точках a и b. Тогда найдётся такая точка , что (1)

Замечание: Формулу(1)можно записать в виде:

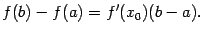
Теорема4 (Коши): Пусть функции и дифференцируемы на интервале и непрерывны при t=α и t=β, причём при всех . Тогда в интервале найдётся такая точка , что

25.Правило Лопиталя.

Т1. (1-е правило Лопиталя)

Пусть ф-ции f(x) и g(x) удовлетворяют условиям:

1. f(x), g(x) дифф в некоторой точке х₀

2. f(x₀)=g(x₀)=0

3. g ꞌ(x₀)≠0 в указанной выше окрестности х₀

4. существует конечный или бесконечный предел

тогда существует = = .

Замечание: Т1 будет верна и в том случае, если f(x) и g(x) не определены в точке х₀, но = = 0.

Замечание 2: Т1 справедлива и в том случае, когда х₀=±∞.

Т2. (2-е правило Лопиталя)

Пусть ф-ции f(x) и g(x) удовлетворяют условиям:

1) f(x), g(x) дифф в некоторой точке х₀

2) f(x₀)=g(x₀)=∞

3) g ꞌ(x₀)≠0 в указанной выше окрестности х₀

4) существует бесконечный предел

Тогда Ǝ = .

или

Раскрытие 0/0. 1-е правило Лопиталя. Если lim(xa)f(x)= lim(xa)g(x), то lim(xa)f(x)/g(x)= lim(xa)f‘(x)/g‘(x), когда предел  конечный или бесконечный.

Раскрытие /. Второе правило.

Если lim(xa)f(x)= lim(xa)g(x)=, то lim(xa)f(x)/g(x)= lim(xa)f‘(x)/g‘(x). Правила верны тогда, когда x,x-,x+,xa-,xa+.

Неопред-ти вида 0, -, 0^0, 1^, ^0.

Неопр. 0, - сводятся к 0/0 и / путем алгебраических преобразований. А неопр. 0^0, 1^, ^0 с помощью тождества f(x)^g(x)=e^g(x)lnf(x) сводятся к неопр вида 0