Пример решения задачи № 6
Найти выигрыш (сокращение пробега) от объединения двух маршрутов
1-2-1 и 1-6-1 в один сборочно-развозочный, которые выполняются на транспортной сети, приведенной в задаче № 3.
По методу Кларка-Райта величина сокращения пробега (выигрыш) при объединении маршрутов o-i-o и o-j-o рассчитывается по формуле:
∆Lij=Loi + Loj - Lij
где Loi - расстояние от пункта о до пункта i;
Loj - расстояние от пункта о до пункта j;
Lij - расстояние между пунктами i и j.
Применительно к данному заданию выигрыш от объединения двух маршрутов 1-2-1 и 1-6-1 в один сборочно-развозочный, будет определяться по формуле:
∆L26=L12 + L16 - L26,
где L12 - расстояние от пункта А (1) до пункта В (2). По схеме транспортной сети
АВ=1 км;
L16 - расстояние от пункта А (1) до пункта F (6). По схеме транспортной сети
АF=6 км;
L26 - расстояние от пункта B (2) до пункта F (6). По схеме транспортной сети
ВF=7 км.
Тогда
∆L26 = 1+6-7 = 0.
Вывод: объединять маятниковые маршруты 1-2-1 и 1-6-1 в один сборочно-развозочный маршрут невыгодно, поскольку выигрыш от их объединения равен нулю: ∆L26 = 0.
Пример решения задачи № 4
Решить транспортную задачу линейного программирования для данных, указанных в нижеприведенной таблице:
-
Ai\Bj
B1
В2
В3
В4
Qi
7
8
8
6
А1
15
11
9
10
8
А2
25
7
6
8
7
А3
30
Qj
10
20
30
25
где Ai - i-й поставщик;
Bj - j-й потребитель;
Qi - объем запасов (ресурсов) у i-го поставщика, тонн;
Qj - объем запросов (потребления) у j-го потребителя, тонн.
В правых верхних углах клеток указаны стоимости перевозок груза Сij от i-х поставщиков к j-м потребителям (или расстояния между i-ми поставщиками и j-ми потребителями Lij).
Транспортная задача линейного программирования (ТЗЛП) заключается в том, чтобы составить оптимальный план закрепления потребителей за поставщиками таким образом, чтобы общие затраты на перевозку грузов от поставщиков к потребителям были минимальны.
1)
Решение ТЗЛП начинается с проверки
баланса
между потребностями потребителей и
запасами поставщиков, чтобы
Qi
=
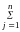Qj.
Qi = 15+25+30=70 т; Qj = 10+20+30+25=85 т.
Поскольку Qi < Qj, т.е. запасы поставщиков меньше потребностей потребителей, то можно сделать вывод, что в задаче баланса нет, поэтому ее следует сбалансировать за счет ввода дополнительного (или фиктивного) поставщика, у которого запасы ресурсов будут равны недостающей до баланса разнице:
Qi ' = Qj - Qi = 85 - 70 = 15 т.
Расстояния от фиктивного поставщика до потребителей обычно принимаются равными наибольшему из имеющихся в задаче расстояний: в данной задаче С4j=11 км. В результате таблица примет вид:
-
Ai\Bj
B1
В2
В3
В4
Qi
7
8
8
6
А1
15
11
9
10
8
А2
25
7
6
8
7
А3
30
11
11
11
11
А4 доп
15
Qj
10
20
30
25
85
Примечание: если бы оказалось, что запросы потребителей больше запасов поставщиков, то следовало бы ввести дополнительного потребителя, потребность которого бы равнялась недостающей до баланса разнице.
2) Далее составляется первоначальный базисный план закрепления потребителей за поставщиками, т.е. заполнение клеток таблицы возможными объемами поставок. Существуют различные методы для его составления.
В данной задаче рассматривается метод минимального элемента (или, другими словами, метод минимальной стоимости). Согласно этому методу в первую очередь необходимо загрузить поставками связи (клетки) с наименьшими расстояниями (стоимостями перевозок) между потребителями и поставщиками. Это основывается на том, что подобная перевозка экономически наиболее выгодна, т.к. сопровождается наименьшими материальными затратами. Причем, клетка загружается таким объемом груза, который равен минимальному значению из запасов поставщика и потребности потребителя:
Qij=min(Qi,Qj).
В данной задаче, рассматривая все возможные связи между потребителями и поставщиками, выбираем клетку с наименьшим расстоянием (стоимостью):
- minСij=С14=6.
Далее рассчитаем возможный объем поставки, включающий минимальное значение из потребности потребителя и запаса поставщика:
Qij=min(Qi=15, Qj=25)=15.
По какой причине выбирается именно наименьшее из двух имеющихся значений? Так как объем поставки не может превышать запроса потребителя или запаса поставщика.
В результате загружаем связь A1B4 поставкой 15 т. После этого запас поставщика A1 оказался полностью исчерпанным, а потребность потребителя B4 частично удовлетворена на 15 т, у него остается еще запрос - 10 т:
Qi ' = Qi - Qij=15-15=0.
Qj' = Qj - Qij=25-15=10.
Т.о. в строке i=1 запас 1-го поставщика полностью исчерпался, поэтому 1-ю строку из дальнейшего рассмотрения исключаем, а запрос 4-го поставщика уменьшаем до 10 т:
-
Ai\Bj
B1
В2
В3
В4
Qi
7
8
8
6
А1
15
15011
9
10
8
А2
25
7
6
8
7
А3
30
11
11
11
11
А4 доп
15
Qj
10
20
30
251085
Из оставшихся связей между поставщиками и потребителями после вычеркивания 1-й строки выбираем связь с наименьшим расстоянием:
- minСij=С32=6.
Загружаемый объем поставки:
Qij=min(Qi=30, Qj=20)=20.
В итоге
Qi ' = Qi - Qij=30-20=10.
Qj ' = Qj - Qij=20-20=0.
Столбец j=2 вычеркиваем из рассмотрения, ресурс поставщика снижаем до 10 т:
-
Ai\Bj
B1
В2
В3
В4
Qi
7
8
8
6
А1
15
15011
9
10
8
А2
25
7
6
8
7
А3
20
301011
11
11
11
А4 доп
15
Qj
10
20030
251085
Из оставшихся связей выбираем связь с наименьшим расстоянием:
- minСij=С34=7.
Загружаемый объем поставки:
Qij=min(Qi=10, Qj=10)=10.
В итоге
Qi ' = Qi - Qij=10-10=0.
Qj ' = Qj - Qij=10-10=0.
Соответствующие строку и столбец вычеркиваем из рассмотрения:
-
Ai\Bj
B1
В2
В3
В4
Qi
7
8
8
6
А1
15
15011
9
10
8
А2
25
7
6
8
7
А3
20
10
3010011
11
11
11
А4 доп
15
Qj
10
20030
2510085
Из оставшихся связей выбираем связь с наименьшим расстоянием:
- minСij=С23=10.
Загружаемый объем поставки:
Qij=min(Qi=25, Qj=30)=25.
В итоге
Qi ' = Qi - Qij=0.
Qj ' = Qj - Qij=5.
Строку i=2 вычеркиваем из рассмотрения, запрос потребителя снижаем до
5 т:
-
Ai\Bj
B1
В2
В3
В4
Qi
7
8
8
6
А1
15
15011
9
10
8
А2
25
2507
6
8
7
А3
20
10
3010011
11
11
11
А4 доп
15
Qj
10
2003052510085
Из оставшихся связей выбираем связь с наименьшим расстоянием:
- minСij=С41=11.
Загружаемый объем поставки:
Qij=min(Qi=15, Qj=10)=10.
В итоге
Qi ' = Qi - Qij=15-10=5.
Qj ' = Qj - Qij=10-10=0.
Столбец j=1 вычеркиваем из рассмотрения, ресурс поставщика снижаем до 5 т:
-
Ai\Bj
B1
В2
В3
В4
Qi
7
8
8
6
А1
15
15011
9
10
8
А2
25
2507
6
8
7
А3
20
10
3010011
11
11
11
А4 доп
10
155Qj
10020030251085
Из оставшихся связей выбираем связь с наименьшим расстоянием:
- minСij=С43=11.
Загружаемый объем поставки:
Qij=min(Qi=5, Qj=5)=5.
В итоге
Qi ' = Qi - Qij=5-5=0.
Qj ' = Qj - Qij=5-5=0.
Соответствующие строку и столбец вычеркиваем:
-
Ai\Bj
B1
В2
В3
В4
Qi
7
8
8
6
А1
15
15011
9
10
8
А2
25
2507
6
8
7
А3
20
10
3010011
11
11
11
А4 доп
10
5
1550Qj
10020030502510085
Затем проверяем необходимое количество поставок по формуле:
N=m+n-1,
где m - число поставщиков;
n - число потребителей.
Если окажется, что число поставок меньше (m+n-1), то следует недостающее количество связей заполнить нулями. Это будет означать, что связи загружены "условными" поставками, равными нулю.
Обычно (но необязательно) в случае, если число поставок меньше (m+n-1), то нулями загружаются до необходимого количества (m+n-1) те связи, где расстояния между потребителями и поставщиками минимальны. А если таких связей несколько, то среди них выбираются любые.
В данной задаче число поставок по количеству загруженных связей:
N'=6,
а необходимое количество поставок в данной задаче должно быть равным:
N = m+n-1=4+4-1 = 7.
Поэтому следует одну недостающую до необходимого количества связь загрузить условной поставкой, равной нулю.
Из оставшихся незагруженными - связи с наименьшими расстояниями - это А1В1 (7) и А3В1 (7). Выберем, например, связь А1В1 и загрузим ее поставкой 0: Q11=0.
Примечание: если окажется, что количество поставок N' больше необходимого количества (m+n-1), значит, следует произвести их перераспределение (см."Перераспределение поставок").
После того как число поставок станет равным необходимому количеству (m+n-1), можно считать, что составлен первоначальный базисный (опорный) план закрепления потребителей за поставщиками:
-
Ai\Bj
B1
В2
В3
В4
Qi
7
8
8
6
А1
0
15
15
11
9
10
8
А2
25
25
7
6
8
7
А3
20
10
30
11
11
11
11
А4 доп
10
5
15
Qj
10
20
30
25
85
3) На следующем этапе решения ТЗЛП происходит проверка базисного плана на оптимальность по условию:
Uij>=0
где Uij - оценочный параметр или критерий оптимальности базисного плана.
Каким образом он рассчитывается? В первую очередь вычисляются все потенциалы поставщиков и потребителей для загруженных связей (т.е. при наличии поставок между потребителями и поставщиками). Это осуществляется с помощью модифицированного распределительного метода МОДИ.