
- •Геомеханика (лекции)
- •Часть I
- •Цели и задачи дисциплины
- •I. Массив горных пород и его особенности
- •Прочностные свойства горных пород
- •Основные факторы, влияющие на прочность горных пород
- •Деформирование и разрушение горных пород. Деформационные свойства горных пород
- •Полная диаграмма деформирования пород. Основные факторы, влияющие на деформационные свойства пород
- •Пластические свойства горных пород. Основные факторы, влияющие на пластические свойства
- •III. Реологические свойства горных пород Основные факторы, влияющие на реологические свойства
- •IV. Распространение упругих колебаний в породах
- •V. Акустические свойства горных пород и массивов. Основные факторы, влияющие на акустические свойства горных пород
- •VI. Состав и строение грунтов. Влияние воды на механическое состояние грунтов
- •Механические свойства грунтов. Основные факторы, влияющие на механические свойства грунтов
- •Основные механические модели массива горных пород и краткая их характеристика Упругая модель массива
- •Пластичная модель массива
- •Упругопластическая модель массива
- •Реологические модели массива
- •Механические характеристики грунтов
Основные механические модели массива горных пород и краткая их характеристика Упругая модель массива
Упругая модель применяется наиболее часто и является основной моделью массива горных пород в геомеханике.
Главное в упругой модели – это линейная связь между напряжениями и деформациями, выраженная законом Гука.
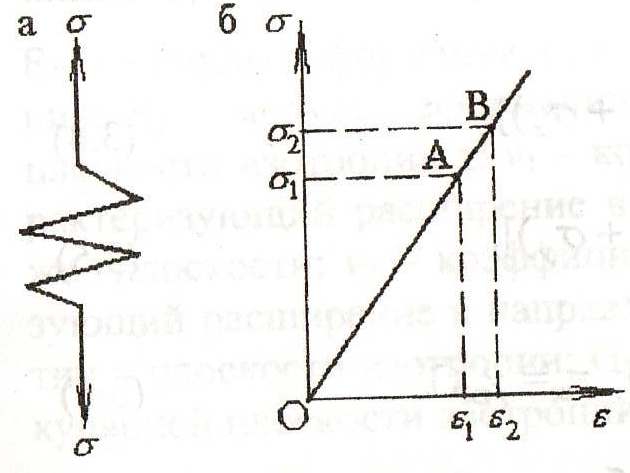
Рис. 7.1. Структурная схема (а) и диаграмма (б) напряжений,
характеризующие упругую модель.
Обобщенный закон Гука описывает объемное напряженное состояние в упругой модели (рис. 7.2).
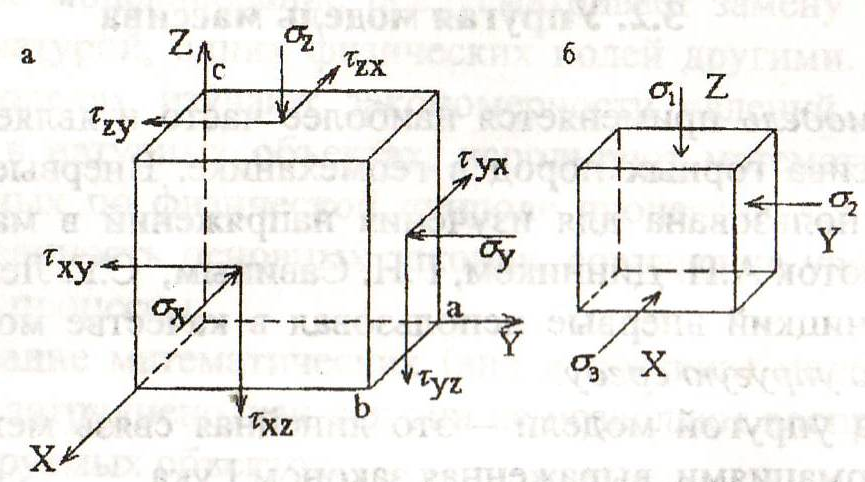
Рис. 7.2. Схема объемного напряженного состояния массива пород.
а) напряжение на произвольных площадках; б) главные напряжения
На основании
принципа независимости действия сил
находим полное относительное удлинение
ребра ав
(рис. 7.2, а) как сумму удлинений при
действиях каждого напряжения
![]() .
.
![]() (7.2)
(7.2)
или, вынося за скобки и ,
![]() (7.3)
(7.3)
Аналогично можно
найти линейные деформации в направлении
осей
![]() и
и
![]() .
.
![]() (7.4)
(7.4)
![]() (7.5)
(7.5)
![]() (7.6)
(7.6)
Уравнения 7.3-7.6 выражают обобщенный закон Гука для изотропного массива горных пород.
Обобщенный закон
Гука для плоского напряженного состояния
(![]() )
имеет вид:
)
имеет вид:
 ,
(7.7)
,
(7.7)
Пластичная модель массива
Пластичная модель (модель Сен-Венана) характеризует процесс деформирования пластических горных пород (грунтов) под действием приложенных нормальных напряжений.

Рис. 7.3. Структурная схема (а) и диаграмма напряжений (б) пластической модели.
1 – отсутствие деформаций; 2 – пластические деформации
Из схемы 7.3. следует условие пластичности горных пород (грунта) Кулона.
![]() (7.8)
(7.8)
где ![]() – напряжения сдвига породы;
– напряжения сдвига породы;
![]() - сцепление породы, т.е. напряжения сдвига
при
= 0;
- угол внутреннего трения породы.
- сцепление породы, т.е. напряжения сдвига
при
= 0;
- угол внутреннего трения породы.
Условие 7.8 называют условием предельного состояния. Графическое выражение этого условия представляет собой паспорт прочности связной горной породы, находящейся в объемном напряженном состоянии (паспорта прочности Кулона-Мора).
Упругопластическая модель массива
Отличие упругопластической модели от пластической заключается в наличие упругих деформаций, которые предшествуют пластическим.

Рис. 7.4. Структурная схема (а) и диаграмма напряжений (б) упругопластической модели:
1 – область упругих деформаций;
2 – область пластических деформаций
![]() (7.9)
(7.9)
Реологические модели массива
Реологические модели отражают свойство ползучести (течения) горных пород, т.е. их способность деформироваться во времени при постоянном напряжении.
Существуют вязкоупругие и вязкопластические реологические модели. Обе включают в себя вязкий элемент Ньютона в виде поршня в цилиндре с вязкой жидкостью.

Рис. 7.5. Вязкий элемент Ньютона
1 – цилиндр тс вязкой жидкостью; 2 – поршень с отверстиями
Согласно закону Ньютона в вязком элементе напряжения пропорциональны скорости деформации (скорости смещения слоев вязкой жидкости).
![]() (7.10)
(7.10)
где ![]() - скорость деформации (градиент скорости
смещения слоев);
- скорость деформации (градиент скорости
смещения слоев);
![]() - коэффициент вязкости, Пас.
- коэффициент вязкости, Пас.
Одна из наиболее распространенных вязкоупругих моделей, модель Максвелла.

Рис. 7.6. Структурная модель Максвелла
Модель Максвелла состоит из пружины, т.е. упругого элемента и последовательно соединенного с ней вязкого элемента Ньютона. Напряжения, приложенные к структурной модели, вызывают в начальный момент мгновенную упругую деформацию пружины, соответствующую закону Гука. В дальнейшем деформация системы растет с постоянной скоростью в результате поддавливания жидкости через отверстия поршня.
Скорость деформации
среды
складывается из скорости упругой
деформации
![]() и скорости вязкой деформации
и скорости вязкой деформации
![]() .
.
![]() (7.11)
(7.11)
отсюда получаем
![]() (7.12)
(7.12)
где ![]() – период релаксации напряжения в данном
теле, т.е. время, в течении которого
напряжения в теле уменьшаются в e
= 2,72 раза.
– период релаксации напряжения в данном
теле, т.е. время, в течении которого
напряжения в теле уменьшаются в e
= 2,72 раза.
При
![]() процесс деформации принимает процесс
ползучести и предыдущее уравнение
примет вид
процесс деформации принимает процесс
ползучести и предыдущее уравнение
примет вид
![]() (7.13)
(7.13)
где ![]() – произвольная постоянная, или упругая
деформация в начальный момент времени.
– произвольная постоянная, или упругая
деформация в начальный момент времени.
Следовательно, рост деформации при постоянном напряжении идет по линейному закону.
Вязкопластические модели учитывают развитие во времени упругих, пластических и вязких деформаций.
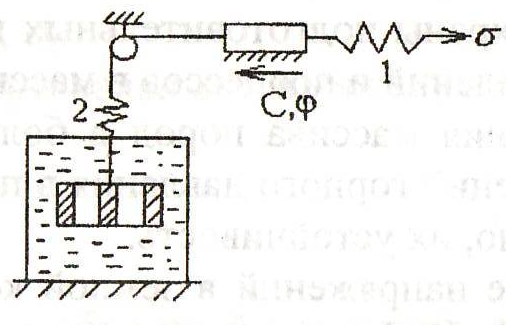
Рис. 7.7. Структурная схема вязкопластической модели Шведова.
Общая деформация такой среды под действием приложенной нагрузки равна
![]() (7.14)
(7.14)
