2 Системы скалярного управления
2.1 Синтез и анализ замкнутой по скорости системы скалярного управления
Таблица 3 – Исходные данные
-
Параметр
Значение
Ед. изм.
Номинальная частота вращения ротора
309,97
с-1
Номинальный момент Мн
354,87
Н·м
Пусковой момент Мп
887,18
Н·м
Критический момент Мкр
1171,08
Н·м
Номинальный ток статора Iн
198,18
А
Критическое скольжение sкр
0,09293
Сопротивление
активное статора RS
0,02257
Ом
активное ротора RR
0,01571
Ом
реактивное статора XS
0,07035
Ом
реактивное ротора XR
0,09715
Ом
Сопротивление взаимоиндукции Xm
5,728
Ом
Полная индуктивность
статора LS
0,01846
Гн
ротора LR
0,01854
Гн
Взаимная индуктивность статора и ротора приведенная к статору Lm
0,01823
Гн
Коэффициент магнитной связи
статора kS
0,9879
ротора kR
0,9833
На рисунке 11 приведена структурная схема системы ПЧ-АД замкнутой по скорости ротора двигателя [3, c. 197].
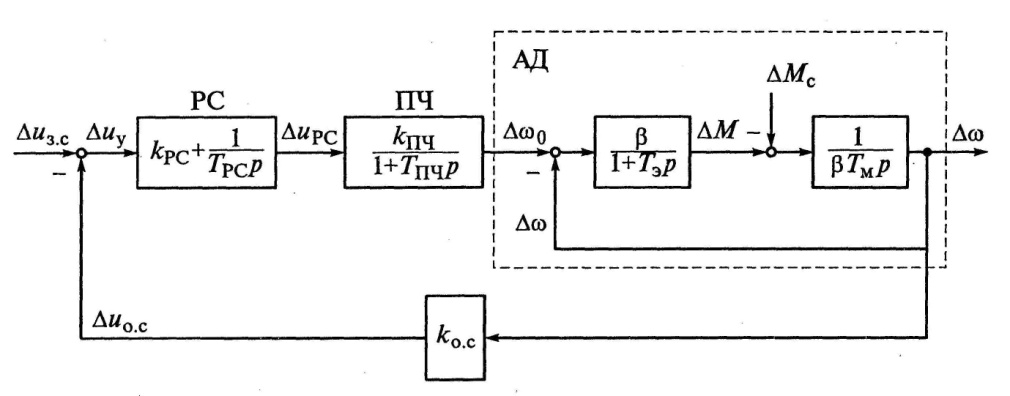
Рисунок 11 – Структурная схема системы ПЧ-АД замкнутой по скорости ротора двигателя
Расчет параметров структурной схемы [3, c. 197].
Модуль жесткости линеаризованной механической характеристики:
Эквивалентная электромагнитная постоянная времени:
Передаточный коэффициент преобразователя частоты:
Расчет:
Расчет коэффициентов обратных связей
Коэффициент обратной связи по скорости:
где
– максимальное напряжение задания,
соответствует 10 вольтам.
Синтез передаточных функций
При синтезе передаточных функций для упрощения расчетов пренебрежем обратной связью по ЭДС двигателя. В следствии чего появится ошибка при регулировании скорости вращения ротора.
Передаточная функция разомкнутого контура регулирования скорости
где
-
суммарный момент инерции привода:
где
- момент инерции двигателя;
- момент инерции механизма, 
Для
расчетов принимаем момент инерции
механизма 
, тогда момент инерции привода равен:
Желаемая передаточная функция контура регулирования скорости настроенного на симметричный оптимум (МО):
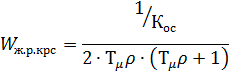
Принимаем
В результате синтеза регулятора получим выражение для регулятора скорости:
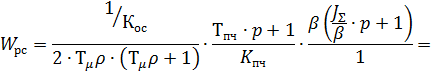
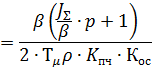
Преобразуем выражения для реализации регулятора в модели. Для упрощения понимания структуры регулятора введем коэффициент:
Рассчитаем данный регулятор:
Тогда регулятор скорости будет выглядеть следующим образом:
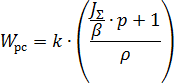
Рассчитаем данный регулятор:
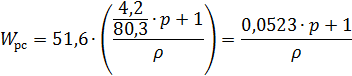
Построим модель ПЧ-АД в абсолютных единицах и смоделируем пуск двигателя. Необходимо также учесть, что данная структурная схема предназначена для управления двигателем на рабочем участке характеристики, так называемое управление в «малом». Следовательно, в пусковом режиме структурная схема не гарантирует получения адекватных данных о переходном процессе при пуске.
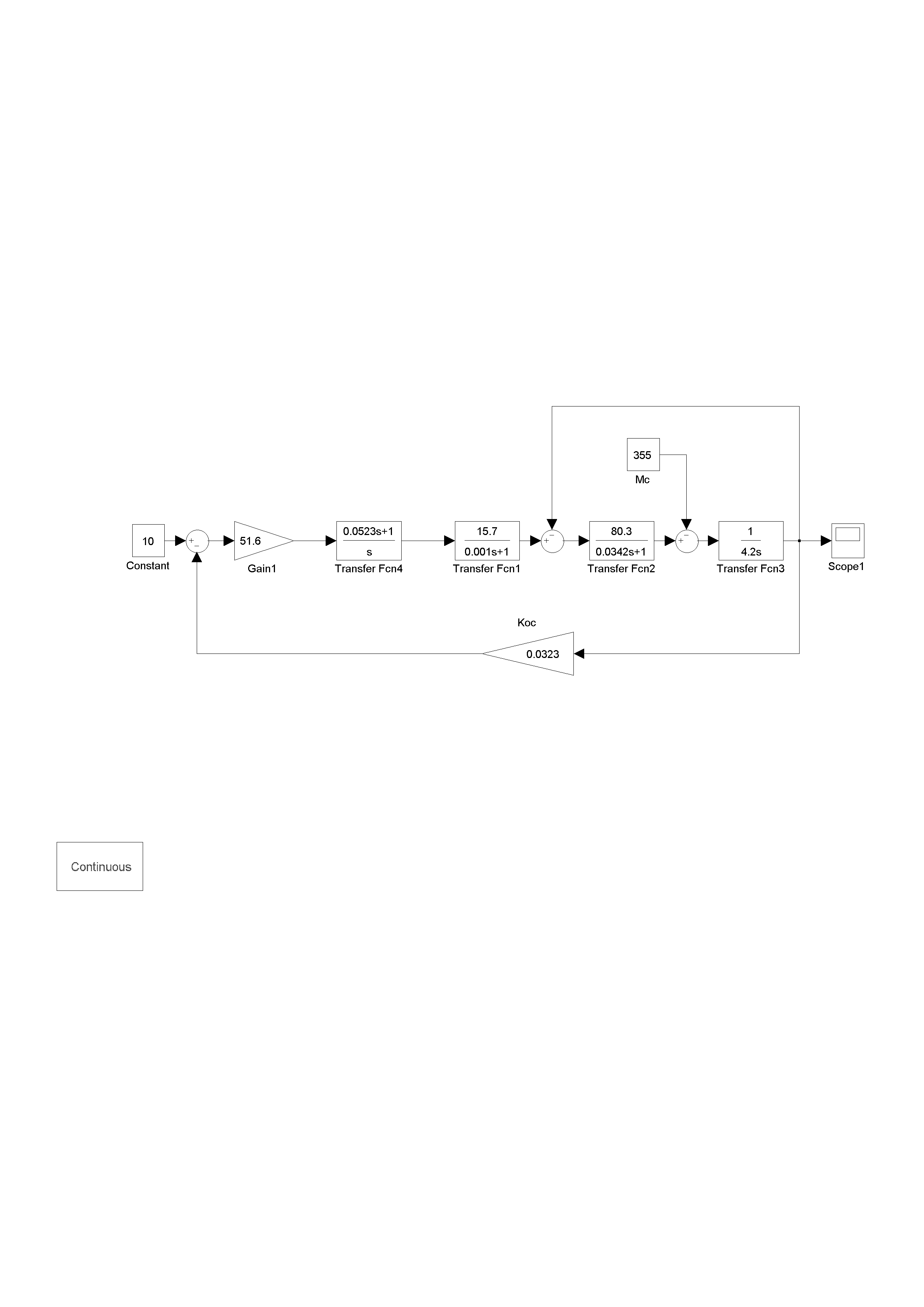
Рисунок 14 - Структурная схема системы ПЧ-АД замкнутой по скорости ротора двигателя в Simulink
Рисунок
15 – Переходный процесс по скорости,
при настройке регулятора на МО
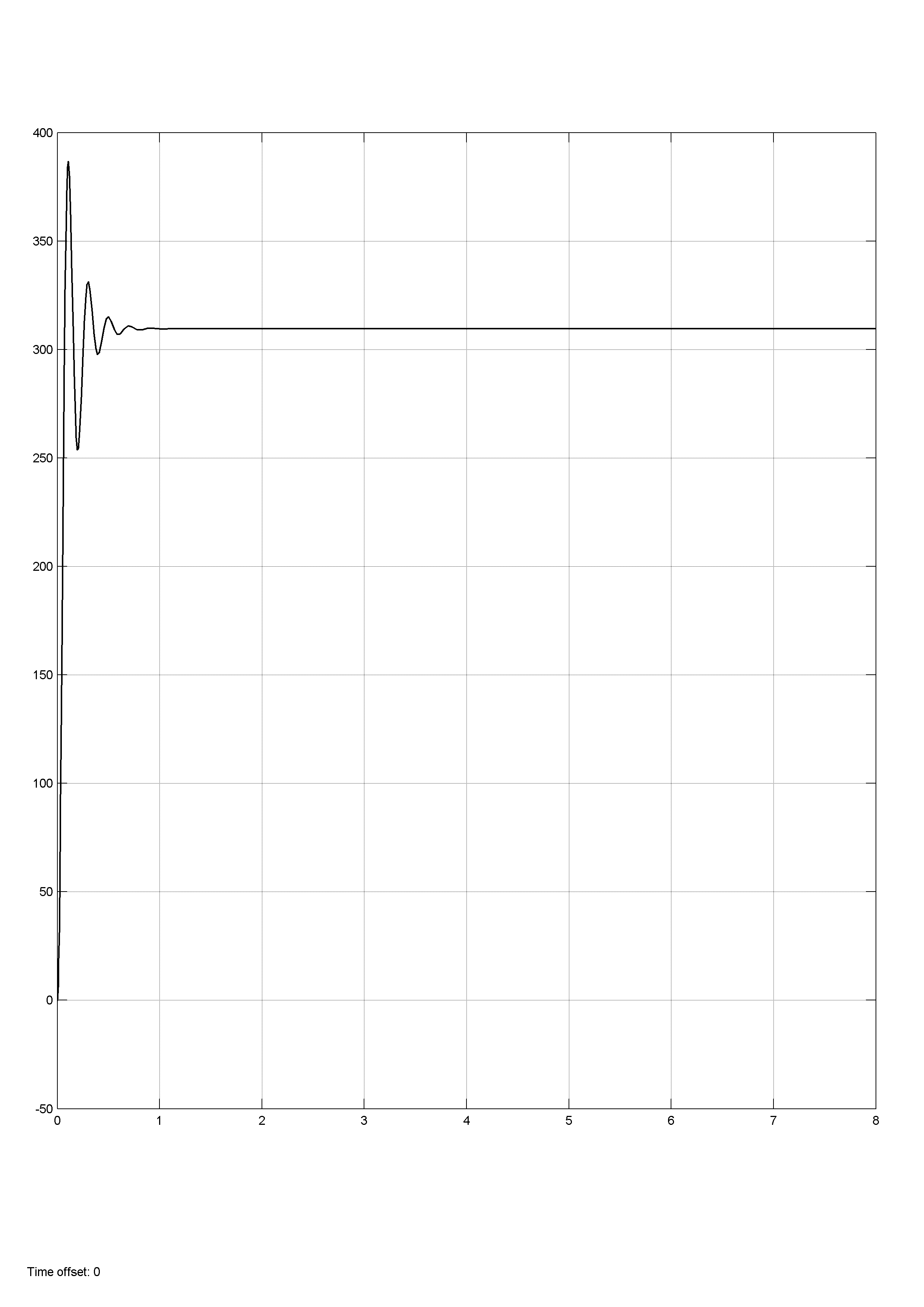
Анализируя полученные результаты (см. рисунок 15) полученные при моделировании делаем выводы:
Пренебрегая обратной связью по скорости внутри двигателя, мы получаем ожидаемую ошибку на валу двигателя.
При регулировании скорости мы не контролируем величину момента на валу двигателя, которая может достигать больших пределов, даже при ограничении на входе ПЧ;
Данная система управления подходит для не ответственных механизмов.
Данная система регулирования имеет смысл лишь в том случае, если регулируется ток статора. Для чего необходимо разделить звено преобразования скорости в момент на два звена. Сигналом промежуточного звена будет ток, по которому необходимо организовать обратную связь.