
- •15 Вопрос
- •16 Вопрос
- •17 Вопрос .Теория прочности.
- •18 Вопрос
- •19 Вопрос
- •20 Вопрос
- •1.1 Температура
- •Рекомендации по определению tR
- •1.2 Давление
- •Рекомендации по определению Рпр
- •21 Вопрос
- •22 Вопрос
- •23 Вопрос
- •2. Расчет на прочность эллиптических днищ и крышек от действия наружного давления по гост 14249-89.
- •24 Вопрос.
- •25 Вопрос.
- •26 Вопрос.
- •27 Вопрос.
- •28 Вопрос.
- •29 Вопрос.
- •30 Вопрос
- •31 Вопрос
- •32 Вопрос. Расчет рубашек с вмятинами или отверстиями
- •2.3.3. Расчет плоских участков
- •33 Вопрос.
- •34 Вопрос
- •35 Вопрос.
- •3.4. Расчет допускаемого давления
- •36 Вопрос.
- •37 Вопрос.
- •38 Вопрос
- •39 Вопрос.
- •40 Вопрос.
- •41 Вопрос.
- •42 Вопрос.
- •43 Вопрос.
- •1. Определение периода собственных колебаний.
- •2. Определение изгибающих моментов от действия ветровой нагрузки.
- •3. Определение расчетных усилий от сейсмических воздействий.
- •44 Вопрос.
- •45 Вопрос.
15 Вопрос
Основное условие существования безмоментной теории прочности – отсутствие причин, вызывающих изгиб.
В основе безмоментной теории лежит аксиома, что оболочки работают на растяжение (сжатие) и не воспринимают изгибающих нагрузок.
Условие применения безмоментной теории прочности:
Сосуд должен состоять из оболочек
 ;
;Оболочка должна быть оболочкой вращения;
Оболочка не должна иметь резких перегибов;
Края оболочки должны быть жестко закреплены;
Нагрузка должна быть равномерно распределенной относительно центральной оси;
Нагрузка должна быть осесимметричной.
Все эти условия должны обеспечиваться конструктивными разработками.
При определении напряжений возникающих в тонкостенных оболочках от действия равномерно распределения внутреннего давления используют метод независимости действия сил. Он заключается в следующем:
Оболочка рассекается в опасных сечениях плоскостями, перпендикулярными центральной оси.
В местах сечения обозначаются известные и неизвестные силы и моменты
действие отсеченных частей заменяется нагрузками
составляется уравнение равновесия действующих сил
определяются неизвестные напряжения или силы
На элемент оболочки действуют следующие силы и моменты:
U – меридиональная сила. Растягивает или сжимает элемент вдоль образующей или меридиана.
Т – кольцевая сила. Растягивает или сжимает оболочку оп параллельному кругу.
М – меридиональный момент. Деформирует оболочку в плоскости, перпендикулярной к меридиану.
К – кольцевой момент. Деформирует оболочку в плоскости, перпендикулярной к кольцевой силе.
Эти силы и моменты вызывают напряжения:
– меридиональные
 ,
,

– кольцевые
 ,
,

Из оболочки выделяем элементарный участок и рассматриваем его равновесие
При действии внутреннего давления стенки тонкостенного сосуда или растягиваются или сжимаются. Элемент выделяется 2-мя плоскостями, перпендикулярными центральной оси и самому элементу. Стенка находится под действием внутреннего давления.
В
элементе оболочке от меридиональных
напряжений возникают силы:
От
кольцевых напряжений:

От
внутреннего давления:

Усилия от внутреннего давления должны быть уравновешены усилиями от меридиональных и кольцевых напряжений.
 (1)
(1)
При решении (1) относительно напряжений получаем первое уравнение равновесия Лапласа:
 (2)
(2)
Недостаток
в том, что две неизвестных –
 и
и
 .
Поэтому для определения одного из этих
напряжений рассматривают уравнение
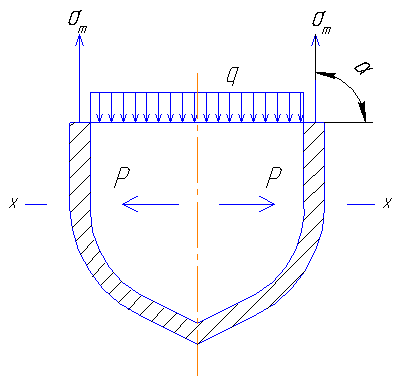
равновесия зоны оболочки. Для этого из
оболочки отсекают зону и рассматривают
её равновесия. На зону оболочки действуют
равномерно распределенные внутренние
давления, на всю внутреннюю поверхность;
и по толщине металла действуют усилия
от меридиональных напряжений.
.
Поэтому для определения одного из этих
напряжений рассматривают уравнение
равновесия зоны оболочки. Для этого из
оболочки отсекают зону и рассматривают
её равновесия. На зону оболочки действуют
равномерно распределенные внутренние
давления, на всю внутреннюю поверхность;
и по толщине металла действуют усилия
от меридиональных напряжений.

 (3)
(3)
(3) – второе уравнение Лапласа
Для
цилиндрической оболочки вращения:
 ,
,
 (4),
(4),
 (5);
(5);
Для
конической оболочки вращения:
,
 (6),
(6),
 (7);
(7);
Для
цилиндрической оболочки вращения:
 ,
,
 ,
(8).
,
(8).
