
- •1. Введение
- •1) Задачи курса сопротивления материалов, реальный объект и расчетная схема.
- •2) Классификация тел по геометрическим параметрам (определения стержня, пластины, оболочки).
- •3) Классификация внешних сил.
- •4) Основные определения.
- •5)Перемещения
- •6) Деформации (абсолютные и относительные, продольные и поперечные).
- •7) Напряжения (нормальное и касательное напряжения), понятие о напряженном состоянии в точке.
- •8) Коэффициент запаса.
- •9) Общий вид условия прочности.
- •10) Внутренние силы. Метод сечений.
- •11) Основные гипотезы о свойствах материала.
- •12) Внутренние силовые факторы в стержне при центральном растяжении-сжатии.
- •13) Нормальные напряжения в поперечных и наклонных сечениях прямого стержня.
- •14) Гипотеза плоских сечений.
- •15) Продольные и поперечные деформации, коэффициент Пуассона.
- •16) Закон Гука при одноосном растяжении-сжатии.
- •17) Перемещения поперечных сечений стержня и его удлинение.
- •18) Построения эпюр продольных сил, нормальных напряжений и осевых перемещений на примере бруса.
- •19) Статически определимые и статически неопределимые задачи на растяжение-сжатие.
- •20)Температурные деформации и напряжения.
- •21) Экспериментальное определение механических характеристик материалов при центральном растяжении и сжатии. Механические характеристики материала.
- •22) Пластические и хрупкие материалы.
- •23) Закон разгрузки и повторного нагружения.
- •31) Осевые, полярные и центробежные моменты инерции.
- •32) Изменение моментов инерции при параллельном переносе и повороте осей координат.
- •33) Главные оси и главные моменты инерции.
- •34) Моменты инерции простых фигур.
- •35) Алгоритм определения положения центра тяжести сечения и вычисления моментов инерции для составных сечений. Применение понятий геометрических характеристик в расчетах.
- •4. Кручение
- •36)Понятие о чистом сдвиге.
- •37) Связь между модулями упругости первого и второго рода и коэффициентом Пуассона.
- •38) Кручение прямого стержня круглого поперечного сечения.
16) Закон Гука при одноосном растяжении-сжатии.
Рассмотрим однородный стержень с одним концом, жестко заделанным, и другим свободным, к которому приложена центральная продольная сила Р (рис. 2.2). До нагружения стержня его длина равнялась l после нагружения она стала равной l + l (рис. 2.2). Величину l называют абсолютным удлинением стержня.
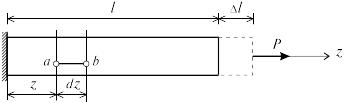
Рис. 2.2
В пределах малых деформаций при простом растяжении или сжатии закон Гука записывается в следующем виде:
= E . (2.3)
Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости материала первого рода. Из совместного рассмотрения уравнений (2.2) и (2.3) получим:
 . (2.4)
. (2.4)
17) Перемещения поперечных сечений стержня и его удлинение.
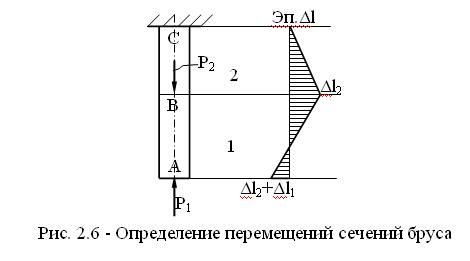
Перемещение любого сечения стержня равно алгебраической сумме абсолютных деформаций всех участков, расположенных между этим и неподвижным сечением (рис. 2.6). Абсолютные продольные деформации определяются из закона Гука
![]()
где N - продольная сила; l - длина участка; F - площадь поперечного сечения бруса; EF - жесткость стержня при растяжении-сжатии. Пример:
Определим абсолютные деформации участков:

где продольную силу определим, как:
 Таким
образом, перемещения сечений стержня
в точках А, В, С равны:
Таким
образом, перемещения сечений стержня
в точках А, В, С равны:
18) Построения эпюр продольных сил, нормальных напряжений и осевых перемещений на примере бруса.
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а).
Делим брус на участки нагружения. ^ Участком нагружения считают часть бруса между внешними силами. На представленном рисунке 3 участка нагружения. Воспользуемся методом Сечений и определим внутренние силовые факторы внутри каждого участка. ^ Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций |
|
в опорах. Участок 1: ΣFz = 0; - 3F + N1 = 0; N1 = 3F. Продольная сила положительна, участок 1 растянут. Участок 2: ΣFz = 0; -3F + 2F + N2 = 0; N2 = = F. Продольная сила положительна, участок 2 растянут. Участок 3: ΣFz = 0; -3F + 2F + 5F - N3 = 0; N3 = 4F. Продольная сила отрицательна, участок 3 сжат. Полученное значение Nз равно реакции в заделке. Под схемой бруса строим эпюру продольной силы (рис. 20.26).
|
^ Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса. |
При растяжении и сжатии в сечении действует только нормальное напряжение. Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. Поэтому напряжение можно рассчитать по формуле
|
где Nz — продольная сила в сечении; А — площадь поперечного сечения |
Нормальные напряжения действуют при растяжении от сечения, а при сжатии к сечению
|
|
Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений. Строится и оформляется такая эпюра так же, как и эпюра продольных сил.
|
Рассмотрим брус, нагруженный внешними силами вдоль оси (рис. 20.5). Обнаруживаем три участка нагружения и определяем величины продольных сил. Участок 1: N1 = 0. Внутренние продольные силы равны нулю. Участок 2: N2 = 2F. Продольная сила на участке положительна. Участок 3: N3 = 2F - 3F = - F. Продольная сила на участке отрицательна. Брус — ступенчатый. С учетом изменений величин площади поперечного сечения участков напряжений больше. |
![]() ;
; ![]() ,
, ![]() ;
; ![]() Ө.
Ө.

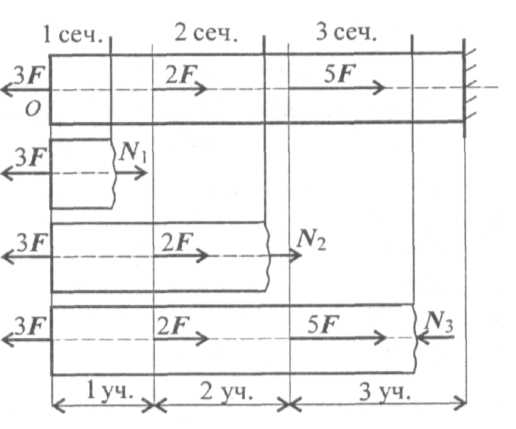 Рис.
Рис. 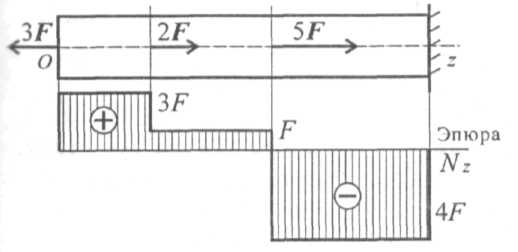
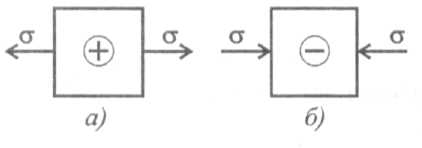
 Рис.
Рис.