11) Основные гипотезы о свойствах материала.

1. Гипотеза о сплошности материала. Предполагается, что материал полностью заполняет занимаемый им объем. 2. Гипотеза об однородности и изотропности. Предполагается, что свойства материала одинаковы во всех точках и в каждой точке — во всех направлениях.

3. Гипотеза о малости деформации (гипотеза относительной жесткости материала). Предполагается, что деформации малы по сравнению с размерами деформируемого тела. 4. Гипотеза о совершенной упругости материала. Все тела предполагаются абсолютно упругими. 5. Гипотеза о линейной зависимости между деформациями и нагрузками. Предполагается, что для большинства материалов справедлив закон Гука, устанавливающий прямо пропорциональную зависимость между деформациями и нагрузками. 6. Гипотеза плоских сечений. Предполагается, что мысленно проведенные плоские сечения, перпендикулярные к оси стержня, в процессе его деформирования остаются плоскими и перпендикулярными к оси. 2. Центральное растяжение (сжатие) прямого стержня

12) Внутренние силовые факторы в стержне при центральном растяжении-сжатии.

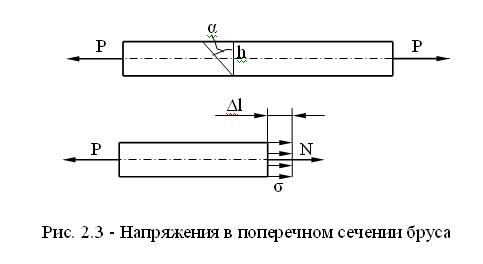
Растяжение – вид деформации, при котором в поперечном сечении стержня возникает внутренняя продольная сила N, при этом длина увеличивается, а ширина уменьшается.

Для определения продольной внутренней силы N используют метод сечений.

Условимся считать эту силу положительной (т.е. присвоим знак «+»), если она растягивает стержень, и отрицательной – если сжимает – правило знаков.

Продольная сила – внутреннее усилие, равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня.

13) Нормальные напряжения в поперечных и наклонных сечениях прямого стержня.

Продольная сила связана с возникающими в этом сечении нормальными напряжениями зависимостью:

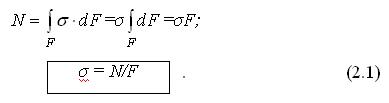
Равномерно распределенные нормальные напряжения     , возникающие в поперечном сечении бруса при центральном растяжении-сжатии, равны отношению продольной силы к площади поперечного сечения.

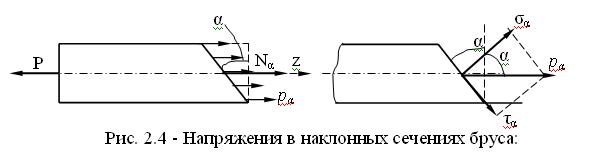
Рассмотрим напряжения в наклонных сечениях бруса (рис. 2.4).

  - угол между наклонным и поперечным сечениями;        - внешняя сила, действующая на брус;       - напряжения в точках наклонного сечения;       - внутренняя продольная сила наклонного сечения;        - площадь наклонного сечения.

Выведем формулы для определения напряжений в произвольных наклонных площадках.

14) Гипотеза плоских сечений.

Поперечные сечения бруса плоские и перпендикулярные продольной оси до деформации остаются таковыми и после деформации. Для проектного расчета размеры поперечного сечения определяются из условия прочности по нормальным напряжениям

15) Продольные и поперечные деформации, коэффициент Пуассона.

Растяжение – это такой вид нагружения, когда в поперечном сечении растянутого тела действуют только продольные силы N.

Деформация – когда деталь изменяет линейные размеры и больше не возвращается в начальное состояние.

Рассмотрим деформацию бруса под действием продольной силы. l – начальная длина, b – начальная ширина, ∆ l – абсолютное удлинение, ∆b – абсолютное сужение.

Относительная продольная деформация Ε:

Ε=∆l/l.

П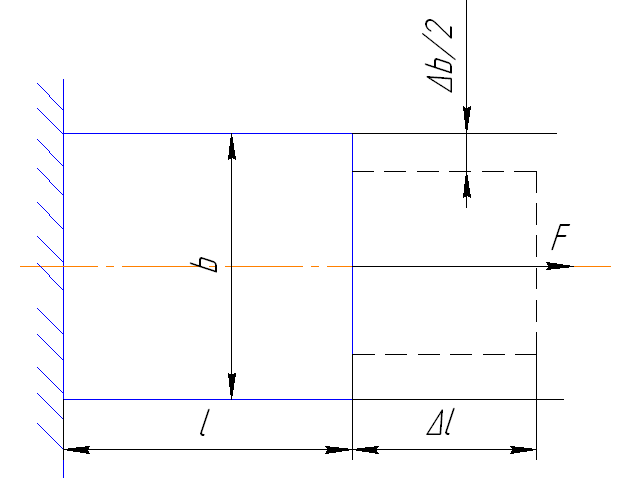 ри растяжении тела происходит изменение его поперечного сечения, т.е. сужение. Линейная (поперечная) деформация:

Ε₁=∆b/b. Е и Е₁ безразмерные величины.

Данные деформации учитывают в точных расчётах.

μ=Ε1/Ε – коэф-т относительной деформации, или коэф-т Пуассона, - хар-ка пластичности материала.