14.Преобразования Лоренца. Следствия из преобразований Лоренца.

В СТО между координатами и временем в двух ИСО существуют соотношения, называемые преобразованиями Лоренца. Если СО движутся друг относительно друга вдоль оси ОХ, то их можно записать в следующем виде.

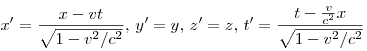
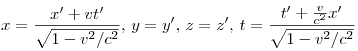
При условии   они переходят в преобразования Галилея.

С учетом преобразований Лоренца принцип относительности можно сформулировать следующим образом: законы, описывающие любые физические явления, во всех ИСО должны иметь одинаковый вид. Этот вывод называется релятивистской инвариантностью законов физики.

Следствия:

1. Если в одной системе отсчета некоторые события происходят в точках x₁ и x₂ в один и тот же момент времени t, то в другой системе отсчета эти события происходят в точках x'₁ и x'₂ в разные моменты времени t'₁ и t'₂:

Понятие одновременности оказывается зависящим от выбора системы отсчета.

2. Если в одной системе отсчета между двумя событиями, происходящими в одной и той же точке, проходит время t, то в другой системе отсчета между этими же событиями проходит время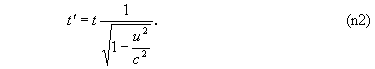

Это соотношение выражает релятивистский эффект замедления времени в движущихся объектах.

3. Если в одной системе отсчета покоящаяся линейка имеет длину l, то в системе отсчета, в которой линейка движется со скоростью u вдоль своей оси, ее длина

Этот эффект называется релятивистским сокращением продольных размеров тела. Поперечные размеры тела не изменяются при переходе в другие инерциальные системы отсчета.

4. Если в одной системе отсчета тело имеет скорость v = (v_x, v_y, v_z), то его скорость v' = (v'_x, v'_y, v'_z) в другой системе отсчета равна

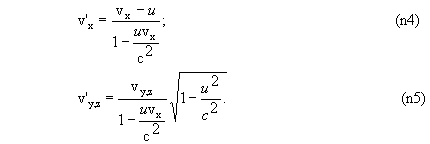
или в трехмерной векторной форме 

5. Из соотношений (n4), (n5) следует постоянство скорости c в различных системах отсчета. Действительно, если вычислить сумму квадратов левых частей этих равенств при условии

v²=(v_x)²+(v_y) ²+(v_z) ²=c², (n6)

получим

v'²=(v'_x)²+ (v'_y)²+(v'_z) ²=c². (n7)

Т. е. скорость c одинакова по величине во всех инерциальных системах отсчета (независимо от направления). Заметим, что направления скоростей v и v' в общем случае различны в разных системах отсчета.

15. Основной закон релятивисткой динамики материальной точки. Закон взаимосвязи массы и энергии.

Масса движущихся релятивистских частиц зависит от их скорости:

                                                                    (39.1)

где m₀ — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в ваку­уме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.

Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона

оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса.

Основной закон релятивистской динамики материальной точки имеет вид

                                                                     

или

                                                                 

где