1. Кинематическое описание движения: материальная точка, система отсчёта, радиус-вектор, перемещение, скорость, ускорение. Скорости и ускорения при прямолинейном равномерном, равнопеременном, ускоренном движении.

2. Угловые характеристики при вращательном движении: угловое перемещение, угловая скорость, угловое ускорение. Угловые характеристики при равномерном, равноускоренном и ускоренном вращательном движении.

3. Криволинейное движение материальной точки: нормальное, тангенциальное и полное ускорение. Соотношение между линейными и вращательными характеристиками

4. Динамика поступательного движения материальной точки. Масса, импульс тела. Законы Ньютона.

5. Закон сохранения импульса (случай замкнутой системы, незамкнутой системы, случай частичного сохранения импульса).

6. Силы в механике (гравитационные, упругости, трения).

7. Энергия как универсальная мера различных форм движения и взаимодействия. Работа постоянной и переменной силы. Мощность.

8. Кинетическая энергия и ее связь с работой внешних сил. Потенциальная энергия м.т. во внешнем силовом поле консервативных сил. Закон сохранения полной механической энергии.

Вопросы с 9 по 15 были даны для самостоятельного изучения по учебникам Трофимой или Савельева:

9. Момент инерции тела, теорема Штейнера (без доказательства).

10. Кинетическая энергия вращения

11. Момент силы, уравнение динамики вращательного движения твёрдого тела

12. Момент импульса и закон его сохранения.

13. элементы специальной теории относительности (СТО): преобразования Галилея. Механический принцип относительности. Постулаты специальной (частной) теории относительности.

14. Преобразования Лоренца. Следствия из преобразований Лоренца.

15. Основной закон релятивисткой динамики материальной точки. Закон взаимосвязи массы и энергии.

16. Электрические заряды. Дискретность электрических зарядов, закон сохранения заряда. Закон Кулона.

17. Электрическое поле, его характеристики: напряженность и потенциал. Силовые линии, напряжённость поля точечного заряда. Работа по перемещению заряда в электрическом поле.

18. Потенциальная энергия заряда. Принцип аддитивности потенциальной энергии. Потенциал электрического поля. Соотношение между напряженностью и потенциалом. Эквипотенциальные поверхности.

19. Циркуляция вектора . Принцип суперпозиции электрических полей.

20. Поток вектора . Теорема Гаусса и ее использование для расчета электрических полей равномерно заряженных плоскости, нити, заряженной сферической поверхности и объёмно-заряженного шара.

21. Проводники в электрическом поле. Поле внутри проводника и у его поверхности. Электростатическая защита.

22. Электрическое поле в диэлектриках. Свободные и связанные заряды. Поляризованность. Диэлектрическая восприимчивость. Диэлектрическая проницаемость среды.

23. Теорема Гаусса для электростатического поля в диэлектрике.

1)Кинематика – изучает движения тел, без учета причин их вызывающих.

Материальная точка – тело, размерами которого можно пренебречь в условиях данной задачи.

Система отсчета – совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение.

Радиус-вектор – вектор, проведенный из начала координат в данную точку.

Перемещение - изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют – вектор, соединяющий положение движущейся точки в начале и в конце некоторого промежутка времени.

Средняя скорость – вектор, равный отношению вектора перемещения к величине промежутка времени, за которое это перемещение произошло.

Мгновенная скорость – векторная величина равная первой производной по времени от радиус – вектора перемещения рассматриваемой точки.

Мгновенное ускорение – векторная величина, равная первой производной по времени от скорости рассматриваемой материальной точки.

Среднее ускорение – вектор, равный отношению вектора изменения скорости к величине промежутка времени, за которое это изменений произошло.

Прямолинейное равномерное движение – движение, при котором тело перемещается с постоянной по модулю и направлению скоростью.

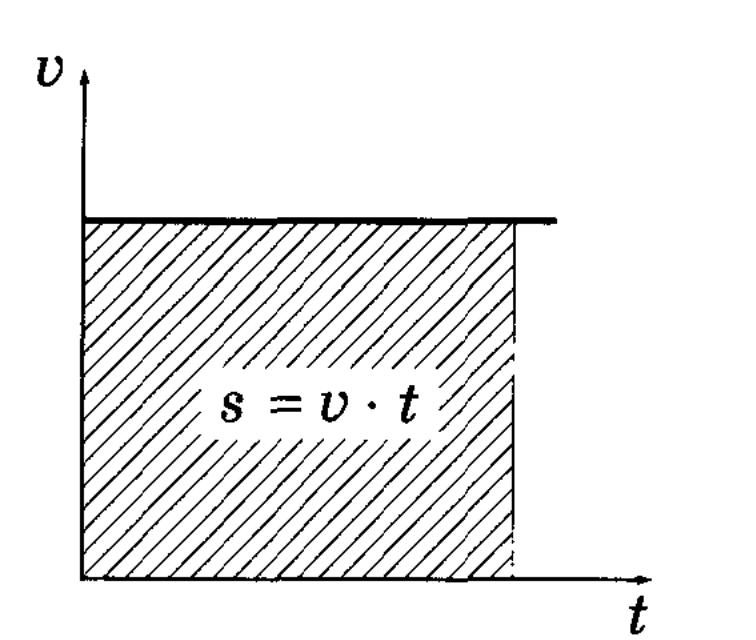
Ускорение а = 0.  скорость  v = const,  путь  s = v∙t, координата  x = x₀    v∙t. Стоит знак плюс, если направление оси ОХ и направление скорости совпадают, и знак минус, если они противоположно направлены.

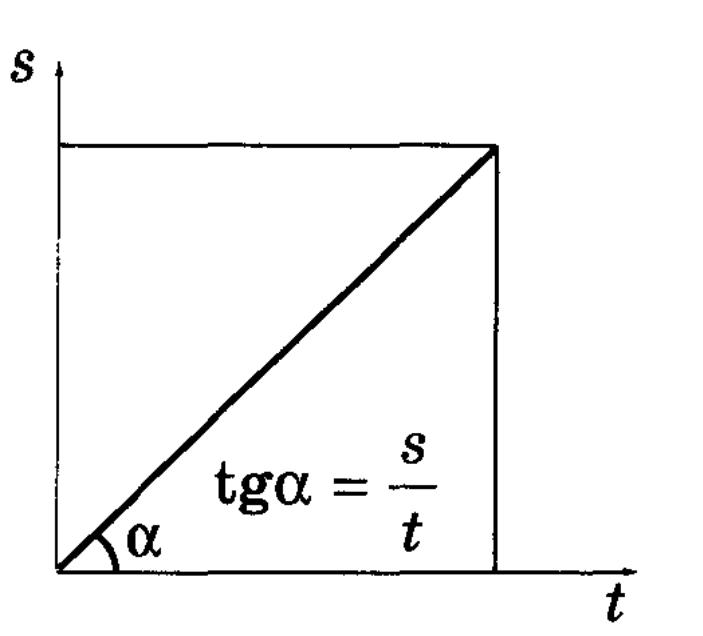
П рямолинейное равнопеременное движение – движение с постоянным ускорением.

Р авноускоренное - модуль скорости увеличивается(a v)

Равнозамедленное – модуль скорости уменьшается(a v)

Ускорение постоянно  а = const,   скорость   ,

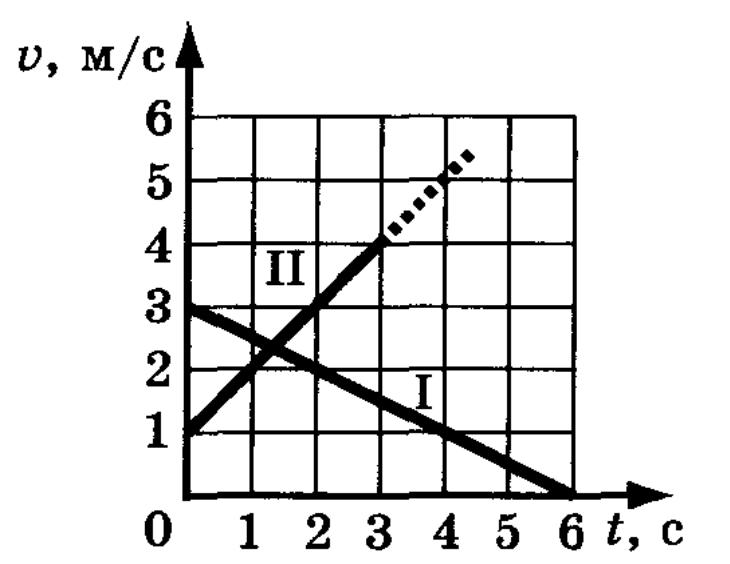
(1- равнозамедленное, 2-равноускоренное)

путь    ,   координата  . +at - равноускоренному движению, минус - равнозамедленному движению.  Перед (v₀t) плюс, если направления v₀ и оси ОХ совпадают, и минус, если они направлены в разные стороны.

1) Вращательное движение - движение, когда  все точки тела описывают окружности, центры которых лежат на оси вращения.

Средней угловой скоростью называется физическая величина, равная отношению углового перемещения к промежутку времени, за которое это перемещение произошло

Мгновенной угловой скоростью называется первая производная от угла поворота по времени:

Угловое перемещение (d φ)– векторная величина, модуль которой равен углу поворота, а направление совпадает с направлением поступательного движения правого винта.

Вектор ω направлен вдоль оси вращения по правилу правого винта, т.е. также как и dφ

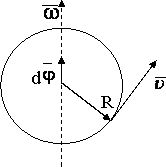
При равномерном движении точки по окружности за любые равные промежутки времени углы поворота ее радиус-вектора одинаковы. Следовательно, при таком движении мгновенная угловая скорость равна средней угловой скорости: ω = ωcp. Угол поворота ∆ω радиус-вектора точки, равномерно движущейся по окружности, равен:

Т-(период) время, за которое материальная точка совершает 1 полный оборот(2π = ωT).

T =

Частота(ν)-число полных оборотов, совершаемых м.т. при вращении по окружности в единицу времени.(Гц) ν=

Циклическая частота (ω) ω= =2πν (рад/с).

У гловым ускорением(β= )- называется векторная величина, равная первой производной угловой скорости по времени. ω направлен вдоль оси вращения, как и вектор dφ.

Β ω, если ω увеличивается. Противоположно направлен, если ω уменьшается.

3) Тангенциальное ускорение — компонент ускорения, направленный по касательной к траектории движения. Совпадает с направлением вектора скорости при ускоренном движении и противоположно направлено при замедленном. Характеризует изменение модуля скорости.

Тангенциальное ускорение при равномерном движении точки по окружности отсутствует ( aτ ).

Центростремительное ускорение – ускорение, направленное в центр окружности.

Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.

Центростремительное ускорение меняет скорость только по направлению, но не меняет по величине. Вектор центростремительного ускорения перпендикулярен вектору скорости.

Полное ускорение точки складывается из касательного и нормального ускорений по правилу сложения векторов. Оно всегда будет направлено в сторону вогнутости тpаектоpии, поскольку в эту сторону направлено и нормальное ускорение.

векторная величина.

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.

Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции Vx и Vy ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени t определяется по формулам :

Частным случаем криволинейного движения – является движение по окружности. Если за любые равные промежутки времени радиус-вектор тела поворачивается на одинаковые углы, а линейная скорость тела по модулю не изменяется (т. е. если |v0|=|v|), движение тела по окружности называют равномерным. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением.

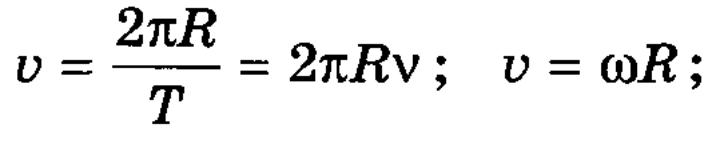
V=

4) Динамика – изучает механическое движение тел, используя представление об их взаимодействиях.

Масса – физическая величина, определяющая инерционные и гравитационный свойства веществ. (кг)

Импульс — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость V, направление импульса совпадает с направлением вектора скорости:

1 закон Ньютона: Существуют такие системы отсчёта, относительно которых материальная точка, при отсутствии внешних воздействий, сохраняет состояние покоя или равномерного прямолинейного движения.

Такие системы отсчёта называются инерциальными.

2 закон Ньютона: В инерциальной системе отсчета сумма всех сил, действующих на тело, равна произведению массы этого тела на векторное ускорение этого же тела (действие на тело силы, проявляется в сообщении ему ускорения).

Величина ускорения, приобретенного под действием силы, зависит от тела, на которое действует сила. Так как большим телам труднее придать ускорение, чем малым, принято пропорциональность между силой и ускорением выражать в следующем виде:

Масса является мерой инертности тела в поступательном движении. Чем меньше инертность тела, тем большее ускорение оно должно приобретать под действием какой-либо определенной силы. Таким образом, второй закон Ньютона можно сформулировать в следующем виде: ускорение тела прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе тела.

3 закон Ньютона: Тела попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей центры масс этих тел (абсолютно-твердые тела), равными по модулю и противоположными по направлению:

Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.

5) Закон сохранения импульса: Геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы. Замкнутая система тел - совокупность тел, взаимодействующих между собой, но не взаимодействующих с другими телами.

P=m₁V₁+m₂V₂=const

Замкнутая система: Если система замкнута(не действуют внешние силы) то импульс системы не меняется с течением времени.

Не замкнутая система: Если внешние силы действуют, но их векторная сумма равно нулю, то импульс системы не меняется с течением времени.

Частичное сохранение импульса: Если пренебречь сопротивлением воздуха, то V_x0=V_x1=V_x2

Если проекция внешней силы, действующая на систему материальной точки, то проекция импульса системы на это направление сохраняется.

6. Силы в механике (гравитационные, упругости, трения).

Сила – величина, являющаяся мерой взаимодействия тел.

По гипотезе Ньютона между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс.

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:

Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной:

G = 6,67·10–11 Н·м2/кг2 (СИ)

Рассчитывать можно, если 1)размеры тел малы, по сравнению с расстоянием; 2)два однородных шара; 3) форма одного шар, размер и масса у одного больше, чем у другого.

Одним из проявлений силы всемирного тяготения является сила тяжести – сила, с которой Земля притягивает к себе тело, находящееся вблизи поверхности. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна

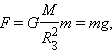
где g – ускорение свободного падения у поверхности Земли:

Сила тяжести направлена к центру Земли (всегда вниз). g – независит от массы тела, объема, плотности и т.д. На полюсах больше, потому что расстояние на полюсах к Земле немного ближе.

При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли.

Сила упругости – сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение. (бывает упругая и пластическая)

Деформация – любое изменение размеров и формы тела. (возможны сжатия, растяжения, сдвига, изгиба, кручения)

Если деформация незаметна и изменением размеров опоры можно пренебречь, силу упругости называют силой реакции опоры.

Закон Гука (сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела). Справедлив только для упругой деформации. Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь F сила натяжения стержня, Δl — его удлинение(сжатие), а k называется коэффициентом упругости (или жёсткостью). Минус в уравнении указывает на то, что сила натяжения всегда направлена в сторону, противоположную деформации.

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как

Величина E называется модулем Юнга и зависит только от свойств тела.

Если ввести относительное удлинение

и нормальное напряжение в поперечном сечении

то закон Гука запишется как

В такой форме он справедлив для любых малых объёмов вещества.

Сила трения – взаимодействие, возникающее в месте соприкосновения тел и препятствующее из относительному движению. (имеют электромагнитную природу)

Трение покоя – сила, препятствующая возникновению движения одного тела относительно другого. (направлена против силы, приложенной, чтобы сдвинуть предмет). Не зависит от площади соприкосновения.

Сила трения скольжения:

Возникает при скольжении данного тела по поверхности другого. Всегда направлена в сторону, противоположную относительной скорости соприкасающихся тел. Зависит от скорости.

Трение качения – если тело не скользит, а катится.

Внешним трением называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении.

Внутренним трением называется трение между частями одного и того же тела, например между различными слоя-ми жидкости или газа, скорости которых меняются от слоя к слою.

Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную направлению движения данного тела относительно другого.

F_тр= μ F_норм = μN

Fтр — сила трения (Ньютон),

μ — коэффициент трения,

Fнорм — сила нормального давления, которое прижимает тело к опоре F (Ньютон)