11. Структурные схемы объектов химической технологии

При изучении сложных объектов удобно расчленять их на ряд звеньев и затем составлять из этих звеньев структурные схемы. Составление структурных схем облегчает составление математических описаний в целом, если предварительно составить математическое описание отдельных его звеньев.

В качестве звеньев в ХТО чаще всего выделяют участки, которые являются либо повторяющимися элементами конструкции аппарата либо отличаются от других участков типом лимитирующего процесса, либо представляют самостоятельную часть конструкции аппарата или установки, либо рознятся по виду переходного процесса (по динамическим свойствам).

Целесообразно проводить расчленение объектов на элементарные звенья по их динамическим свойствам.

Определение динамических характеристик звеньев и их сравнение обычно проводится по изменению входных величин по типовым законам, т.е. в качестве входных возмущений выбирают стандартный ступенчатый или стандартный импульсный сигналы. Соответственно элементарные звенья описываются дифференциальными уравнениями или передаточными функциями.

Общая (эквивалентная) передаточная функция будет зависеть от количества звеньев, их передаточных функций, а также порядка их соединения между собой.

В структурной схеме каждый элемент (звено) обозначается прямоугольником, а связи между ними стрелками, показывающими направление прохождения сигналов. Кружки на схемах с указанием знака сигнала – алгебраическое сложение сигналов.

Различают структурные схемы:

1)последовательного соединения

2)параллельного соединения

3)схемы с обратной связью

Последовательное соединение элементов

Для цепочки из n последовательно соединенных элементов получим:

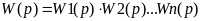
Т.о. передаточная функция цепочки последовательно соединенных элементов равна произведению передаточных функций этих элементов.

Параллельное соединение элементов

Предположим, что 2 элемента соединены параллельно. Они характеризуются передаточными функциями W1(p) и W2(p). Тогда в соответствии со структурной схемой можно записать следующее выражение:

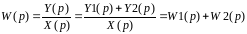
Для n элементов соединенных параллельно получим:

Соединение элементов по схеме с обратной связью

Д ля получения передаточной функции такого соединения с передаточными функциями W1(p) и W2(p) воспользуемся записанными в соответствии с рисунками очевидными равенствами

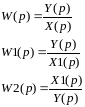
- при положительно обратной связи (обратное воздействие усиливает процесс)

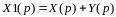
- при отрицательной обратной связи (обратное воздействие замедляет процесс)

Решая эти уравнения получаем 2 выражения для передаточной функции:

При положительной обратной связи

При отрицательной обратной связи

12. Применение операционного исчисления при решении дифференциальных уравнений. Передаточная функция.

Стадии составления ДУ:

1. Изучение сущности процесса и по возможности становление наиболее четкого представления о его механизме, а так же выяснение законов, которыми можно охарактеризовать изучаемый процесс.

2. Выбор дифференцируемого элемента системы (например, элементарный объем dV) и математическая запись того, что происходит в дифференцируемом элементе за время dt с переменной процесса.

3. Составление материального и энергетического балансов, связывающих дифференциальное изменение различных переменных, исходя из общего признака.

[приход] - [расход] = [накопление]

Операционные исчисления устанавливают некоторые свойства операционного соответствия или правила преобразования по Лапласу, которые следует рассматривать как прием, позволяющий относительно просто решать ДУ.

Пример:

Известно, что функцию можно определить как соответствие между множествами чисел, т.е. y=f(x) (множеству чисел х соответствует определенное множество чисел y), но соответствие может быть не только между величинами, но и между функциями, при этом функция одного множества называется оригиналом, а соответствующая ей функция с другим множеством – изображением.

f(t) → Ф(р)

оригинал соответствует изображение

Возможны различные способы преобразования функции f(t) в соответствующие функции комплексной переменной р.

Один из таких методов преобразования по Лапласу, который позволяет упростить вычисление действия с исходной функцией, т.е. позволяет оперировать алгебраическими уравнениями взамен ДУ.

L[f(t)] = Ф(р) =

где L – символ прямого преобразования по Лапласу;

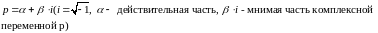
Для большинства видов известных функций преобразование Лапласа каждый раз не выполняют, а используют специальные таблицы.

Для тех функций, вид которых неизвестен обратное преобразование Лапласа (осуществляется с помощью следующих формул):

Но вычисление этого интеграла сопряжено с большими трудностями, поэтому предварительно используют преобразования для того, чтобы привести его к виду удобному для нахождения оригинала по таблице соответствия.

Для преобразования ДУ используют следующие свойства операционного соответствия:

1. Свойство однородности

Если временная функция умножена на постоянную величину, то изображение должно быть умножено на ту же постоянную величину.

2. Свойство сложения

Сумма оригинала соответствует сумме изображений.

3. Изображение интеграла

Операция интегрирования в области действительных переменных соответствует операции деления в области комплексной переменной

4. Изображение производных

Операция дифференцирования в области действительной переменной соответствует операции умножения в области комплексной переменной. При нулевых начальных условиях n-му дифференцированию оригинала соответствует умножения изображения на pⁿ.

5. Изображение функции с запаздыванием

Смещение аргумента оригинала на постоянную величину соответствует умножению изображения на .

Преобразование ДУ проводится с использованием правила соответствия и состоит в переходе от независимой переменной t к комплексной переменной р. Т.о. получают операторную форму записи уравнений. Решением операторного уравнения является изображение искомого решения. Чтобы найти решение в пространстве оригинала необходимо выполнить обратное преобразование Лапласа.

Последовательность решения дифференциального уравнения с использованием преобразования по Лапласу.

1. Приведение исходного уравнения к операторной форме (использование правила и таблицы преобразований по Лапласу)

2. Решение операторного уравнения

3. Нахождение решения исходного уравнения по решению операторного уравнения (использование таблиц преобразований по Лапласу или формула)

В результате действий с ДУ в операторной форме можно получить передаточную функцию, которая широко используется для характеристики исследуемого объекта как эквивалент ДУ.

Пример:

Преобразуем ДУ 2-го порядка

где y и y_bx – соответственно выходная и входная величины; - постоянные коэффициенты.

В результате преобразований по Лапласу:

Передаточная функция W(p) объекта определяет динамические свойства объекта, зная ее можно найти решение ДУ описывающего объект. Для этого необходимо совершить обратное преобразование по Лапласу.

При использовании передаточных функций упрощается вид математического описания объекта и облегчается работа.

Если объект представить как совокупность элементарных звеньев, то его характеристику можно составить передаточные функции этих элементов.