Преобразование Лапласса. Свойства операционного соответствия.
Операционные системы устанавливают некоторые св-ва операционного соответствия или правила преобразования по Лаплассу, кот. надо использ. Как прем, позволяющий просто решить ДУ, т е:
Функцию можно определить, как соответствие между множеством чисел, т.е. y = f(x) Множеству чисел х соотв-ет множество чисел у. Но соответствия могут быть не только между величинами, но и между функциями. При этом ф-ция 1-го множества наз. оригиналом, а соответствующая ей ф-ция с др. множества – изображением: F(t) → Ф(Р) (→ - это значит «соответствует»).
Возможны разн. способы преобразований переменной t, соответствующей комплексной переменной Р. Это преобразование по Лаплассу, кот. позволяет упростить вычислительные действия с исходной ф-цией, т.е. позволяет оперировать алгебр. уравнениями в замен ДУ.
Преобразование по Лаплассу:
L
– символ прямого преобразования по
Лаплассу; Р =
(
);
– действительная
часть;
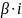- мнимая часть комплексной переменной
Р)
Ограничения на временную ф-цию: f(t) = 0 при t < 0. Для большинства ф-ций преобраз. по Лаплассу не выполняют, а использ. таблицы. Для ф-ций , вид кот. не известен, обратное преобраз. Лапласса:
Его трудно вычислить, поэтому сначала используют любые преобразования полученного изображения, чтоб привести его к виду удобного для нахождения оригинала по табл. соответствия.
Для преобразования ДУ использ. свойства операционного соответствия (ОС):
Св-ва однородности:
или
Если временная ф-ия умножена на постоянную величину, то изображение д. б. умножено на ту же величину.
Св-ва сложения:
или
Сумма оригиналов соотв-ет сумме изображений.
Изображение интеграла:
или
Операционное интегрирование в области действительн. переменных соответствует операции деления в области комплексных переменных.
Изображение производных:
или
или
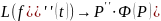
Операционной дифференциации в области действительной переменной соотв-ет операционное умножение в области комплексной переменной. При нулевых начальных условиях n-ому дифференцированию оригинала соотв-ет умножение изображения на Р.
Изображение функции с запаздыванием:
или
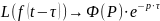
Ситуация аргумента
оригинала на постоянную величину
соотв-ет умножению изображения на
.
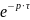Преобразования ДУ проводят
с использованием правил соответствия
и состоит в переходе независимой
переменной t
к комплексной переменной Р,
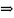Получают
операторную форму записи ДУ.
Решением операторного уравнения является
изображение искомого решения. А что б
найти решение в пр-ве оригинала надо
выполнить обратн. преобразования
Лапласса.
Последовательность решения ДУ: - приведение исходного уравнения к операторной форме (преобраз. по Лаплассу); - решение операторного уравнения; - нахождение решения искомого уравнения по решению операторного.
В результате действия ДУ в операторной форме можно получить передаточную функцию, кот. используется для характеристики исследуемого объекта, как эквивалент ДУ.
Пример: преобразуем ДУ 2-го порядка
Преобразуем по Лаплассу:
или
Обратн. преобразования:
)
W(P) – передаточная функцмя, определяет динам. свойствава объекта; a – постоян. коэф-ты; у, хвх – выходные и входные величины.