40. Экспериментальное изучение распределения времени пребывания элементов потока. Интегральная и дифференциальная функции распределения времени пребывания элементов потока.

В аппаратах хим технологии в результате действия кинетических, гидродинамических, а также факторов тепло и массаобмена в общем случае имеют неравномерность распределения частиц потока во времени, как по сечению потока так и вдоль потока вследствие поперечного и продольного перемешивания. При этом степень неравномерности потока характеризует структуру среды потока.

Степень неравномерности распределения частиц в потоке во времени можно оценить по распространению вещества или по концентрации в-ва в потоке, отсюда задача отыскания кривой на выходе из аппарата в виде изменения концентрации во времени после внесения возмущения в поток на его входе.Возмущающим воздействием может быть введением в аппарат вместе с поступающим потоком,какого-либо в-ва(индикатора трассера)которое не реагирует со средой(наибольшее распространение получили ступенчатые или импульсные сигналы)

При этом реакция объекта определяется фиксированием изменений во времени содержание индикатора в потоке на выходе из аппарата,что позволяет дать оценку структуры потока и определить модель для этого потока.В качестве индикатора используют подкрашенные инертные газы или жидкости,растворысолей,флоарисцирующиепримеси,радиактивныеизотопы,при соблюдении обязательного требования,чтобы они не притерпевали физико хим. Изменений в потоке.

В хим. Технологии р-ция объектов на стандартные входные сигналы имеют специальное название.При стандартном ступенчатом сигнале на входе функции отклика на выходе из аппарата,представляет собой зависимость,кот. Называют F-кривой(Fкр) или интегральной кривой

Графическое изображение Fкривой представляют в безразмерных коорд.Для этого концентрацию индикатора в потоке на выходе(с) относят к его начальной концентрации(С₀) и откладывают по оси ординат значение Fкр=С/C₀

Также используют понятие безразмерного времени

t-натуральное время

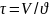
-среднее время пребывания частиц потока в аппарате

–объем аппарата

-объемный расход жидкости

Типичная форма отклика изображена на рисунке на стандартный импульсный сигнал

При импульсной подаче трассора,на входе системы получается Скр(импульсная хар-ка) или диф. Кривая

По координатным осям в кот. Обычно строят Скр аналогично предыдущему случаю откладывают безразмерные ед.При этом условии площадь ограничена Скр=1

По форме или ввиду Скр и Fкр определяют структуру потока в аппарате.Математическая связь между интегральной и диф. Кривой опред. Следующими соотношениями

Метод установления модели потока на основе информации его структуре состоит в том,что фиксирует реакцию объекта на выходе и затем полученные выходные кривые сравнивают с аналогичными кривыми типовых моделей.По результатам совпадений ил отклонений дают оценку структуре исследуемого потока и строят модель отражающую гидродинамику данного потока.

41. Критерии проверки статистических гипотез. Проверка однородности дисперсий.

Нуль-гипотезаН₀: между обеими выборками нет существенной разницы, обе они принадлежат одной генеральной совокупности, а имеющиеся различия обусловлены случайным характером выборок, например, влиянием случайных ошибок.

Обычная процедура проверки гипотез заключается в следующем:

1) по выборочным данным рассчитывается критерий проверки;

2) полученное значение критерия сравнивают с критическим значением, находимым из таблиц. Критическое значение каждого конкретного критерия определяется уровнем значимости и числом степеней свободы, по которому были рассчитаны величины, входящие в критерий.

Рассмотрим некоторые часто встречающиеся критерии проверки гипотез.

Критерий исключения грубой ошибки. Если результаты эксперимента получены из-за грубой ошибки, то их необходимо отбросить, не подвергая никаким статистическим оценкам. Необходимо произвести проверку резко выделяющихся значений.

Критерий проверки имеет вид

где x_под – «подозрительный» результат (наибольший или наименьший);

– среднее, полученное по формуле;

S – среднеквадратичное отклонение; при этом в расчет х иSвключается «подозрительный» результат;

n – количество измерений.

Полученное значение критерия сравнивают с табличным.Также можно использовать, критерий Ирвина λ, который основан на разности x_n и x_n+1 (двух наибольших значений СВ):

Если полученное значение λ_p больше значения, соответствующего табличному λ_кр то его следует оставить.

Критерий Пирсона χ². Для проверки гипотезы о соответствии эмпирического распределения СВ теоретическому наиболее часто применяют критерий Пирсонаχ²

Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что СВd имеет данный закон распределения заданный функцией F(d) или плотностью вероятности f(d). Назовем этот закон распределения «теоретическим».

Зная этот закон, можно вычислить ожидаемое число отказов изделия в определенных интервалах, на которые разбить время испытания.

В результате получим теоретический ряд частот в k интервалах времени испытаний:

Подсчитаем также число отказавших изделий в этих же интервалах в нашем опыте и получим экспериментальный ряд частот

Для проверки согласованности теоретического и экспериментального распределений подсчитывается мера расхождения χ².

и число степеней свободы v=k–f, где f – число ограничений. Число ограничений равно числу параметров распределения, увеличенному на единицу. Для распределения Пирсона составлены специальные таблицы.

Критерий Колмогорова λ. Критерий Пирсона применяют только в тех случаях, когда число наблюдений (n≥25). Если теоретические значения параметров распределения известны, то лучшим критерием является критерий Колмогорова.

Составляют разность между накопленными теоретическими и эмпирическими суммами и находят максимальное значение этой разности, вычисляя величину D по формуле:

Где , – разность функций экспериментального и теоретического распределения СВ.

Коэффициент λнаходят по формуле:

Пользуясь табличными данными для вычисленного значения λ, определяют вероятность P(λ) – вероятность того, что гипотетическая функция выбрана правильно.

Критерий Фишера F. Прежде чем сравнивать средние значения двух выборок, необходимо убедиться в равенстве их дисперсий. При нормальном законе распределения СВ для проверки гипотезы о равенстве (однородности) выборочных дисперсий в качестве критерия используется статистика, которая равна отношению двух независимых оценок дисперсий генеральной совокупности и , имеющих степень свободы соответственно v₁иv₂, т.е.

При этом должно выполняться условие , где – большая величина выборочной дисперсии в двух выборках.

Найденное значение сравнивается стабличным при заданном уровне значимости p и степенях свободы v₁=n₁–1 иv₂=n₂-1. Если F<F_кр, тогда гипотеза о равенстве выборочных дисперсий принимается.

Критерий КохренаG. Если число параллельных опытов в сериях одинаково, то однородность дисперсий нескольких выборок проверяется с помощью критерия КохренаG по формуле:

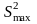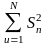где – максимальная дисперсия, а – сумма всех дисперсий выборок, N – число выборок, n – номер выборки.

Если расчетное значение G больше табличного G_кр (при уровне значимости α и степенях свободы v₁=n₁–1 для числителя и v₂=Nдля знаменателя), то гипотеза о равенстве (однородности) дисперсий отвергается.

Если проверка по критериям Фишера и Кохрена покажет, что для оценок дисперсий можно принять нуль-гипотезу, оценки называют однородными; эту процедуру часто называют проверкой однородности дисперсий. Однородные оценки можно усреднить – найти единую оценку дисперсии по всей совокупности измерений; для этого пользуются формулой:

Критерий Стьюдента t. Для проверки гипотезы о равенстве двух выборочных средних значений СВ, имеющей нормальный закон распределения, используют критерий Стьюдента t.

Нуль-гипотеза здесь: средние значения в двух сериях измерений являются оценками одного и того же генерального значения (математического ожидания, истинного значения).

Если серии измерений, в которых получены средние, сделаны с разной точностью (с разными дисперсиями), то процедура сравнения средних резко усложняется. В этих случаях можно рекомендовать специальные методы. Если дисперсии однородны и найдена общая оценка, тогда проверка проводится по критерию Стьюдента

где п₁и n₂– числа измерений в первой и второй сериях; s– единая оценка стандартного отклонения по всей совокупности измерений.

Критическое значение tзависит от v и α.