33 Дробный факторный эксперимент (дфэ). Генерирующее соотношение, определяющий контраст

Увеличение количества факторов в ПФЭ приводит к резкому увеличению числа опытов:ПФЭ 2⁶ – требует 64 опыта,2⁷ – 128 опытов.

Точность модели увеличивается, однако увеличиваются затраты средст и времени. В целом для получения точных оценок коэффициентов регрессии можно обойтись меньшим количеством опытов используя метод ДФЭ, который является частью ПФЭ (1/4,1/8).

Сокращение числа опытов приводит к появлению корреляции между некоторыми столбцами матрицы планирования, что не позволяет раздельно оценивать эффекты факторов и эффекты взаимодействий, следовательно оценки получаются смешенными (оценки в которых учитывается линейный эффект и эффект взаимодействия).

Генерирующее соотношение – соотношение, которое показывает какие взаимодействия заменены новыми факторами (оно генерирует или создает дробную реплику).

34. Проверка гипотез о значимости коэффициентов и адекватности уравнения регрессии, построенного по данным пассивного эксперимента

Для проверки значимости коэффициентов регрессии используют критерии Стьюдента. В процедуру проверки входит:

1. вычисление дисперсии коэффициентов регрессии

S_bi² =S₀/N

где N – число опытов в матрице планирования.

2. Составление отношений

t_bi= │b_i│/ S_bi > t_кр

Здесь S_bi = квадратный корень из S_bi²

Значения критерия находят из таблицы для выбранного уровня значимости и числа степеней свободы (ν = N^* (m -1), N – количество групп параллельных опытов.

Для проверки адекватности модели используют критерий Фишера:

где F_кр – табличное значение для определенного уровня значимости и степ.свободы ν1 = N - 1, ν2 = N^* (m -1).

Остаточная дисперсия

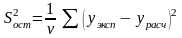
35 Экспериментальное изучение распределения частиц потока во времени

В аппаратах химической технологии в результате действия кинетических, гидродинамических, а также факторов теплообмена и массообмена в общем случае имеет неравномерность распределения частиц потока во времени, как по сечению потока, так и вдоль потока, вследствие поперечного и продольного перемешивания.

При этом степень неравномерности потока характеризует структуру среды и структуру потока.

Степень неравномерности распределения частиц в потоке во времени можно оценить по распределению вещества или по концентрации вещества в потоке. Отсюда задача отыскания структуры среды сводится к отысканию кривой на выходе из аппарата, в виде изменения концентрации во времени после внесения возмущения в поток на его входе. Возмущающим воздействием может быть введение в аппарат вместе с поступающим потоком какого-либо вещества (индикатора, трассера), кот. не реагирует со средой (наибольшее распространение получили ступенчатые и импульсные сигналы).При этом реакция объекта определяется фиксированием изменений во времени содержанием индикатора в потоке на выходе из аппарата, что позволяет дать оценку структуры потока и определить модель для этого потока. В качестве индикаторов используют подкрашенные инертные газы или жидкости, растворы солей флуарисцирующие примеси, радиактивные изотопы при соблюдении обязательного требования, чтобы они не претерпевали физико-химических изменений в потоке.

В химической технологии реакции объектов на стандартные входные сигналы (ступенчатый и импульсный) имеет специальное название. При стандартном ступенчатом сигнале на входе функция отклика на выходе представляет собой зависимость, которую называют F кривой (F_кр) или интегральной кривой.

Графики

Графическое изображение F кривой представляют в безразмерных координатах. Для этого концентрацию индикатора в потоке на выходе относят к его начальной концентрации С₀ и откладывают по оси ординат значение F_кр = C/C_{0 ,} а также используют понятие безразмерного времени

Θ = t/τ,

где t – натуральное время, τ – среднее время пребывания частиц в аппарате (τ = V/ν, где V – объем аппарата, ν – объемный расход жидкости).

Типичная форма отклика изображена на рисунке.

При импульсной подаче трассера на входе системы получается С кривая (импульсная характеристика) по координатным осям в которой обычно строят С кривую аналогично предыдущему случаю откладывая в безразмерных единицах. При этом условная площадь ограниченная С кривой равняется 1. По форме С и F кривые определяют структуру потока в аппарате.

Связь между дифференциальной и интегральной кривой определяется соотношением:

Метод установления модели потока на основе информации о его структуре состоит в том, что фиксируют реакцию объекта на выходе и затем получают выходные кривые, сравнивают с аналогичными кривыми типовых моделей. По результатам совпадений или отклонений дают оценку структуре исследуемого потока и строят модель отражающую гидродинамику данного потока.