25.Типовые химико-технологические процессы.Характеристики объектов химической технологии.

Все ХТП по степени влияния возмущающих параметров подразделяются на 2 группы:

1.детерминированные

2.стохастические

Детерминированные- Процессы ,которых определяющие величины изменяются вполне определимо, но по определенным закономерностям при этом предполагается, что значение выходных величин определяется заданием входных и управляющих воздействий.

Стохастические - процессы, в которых , изменение определяющей величины происходит случайным образом.

С целью выделения тепловых пр-сов ХТ и определения их природы используют след. критерии:

1.общность материала описания(модели пр-са)

2.общность аппаратурно- технологического процесса

3. особенностей автоматизации управления пр-са.

ПО характеру материало-энергетич. связей все про-сы делят на виды:1.гидродинамические(перемещение газов в трубопроводах и аппаратах, разделение суспензий) 2.тепловые(нагревание, охлождения, конденсации) 3.диффузионные (массообменные) - связаны с перемещением в-в в различных состояниях из одной фазы в другую. 4.механические (дробление ,грохочение) 5.химические (опр. законами кинематики)

Объекты ХТ могут быть описаны статическими и динамическими х-ками представляя между собой взаимосвязь входных выходных параметров. Статические х-ки определяют зависимость выходных параметров от входных в остановившемся во времени режиме работы обьекта. Зависят: 1.ф-хим. Свойств перерабатываемого в-ва. 2.х-ки и степени достижения равновесия пр-са. 3.конструктивного оформления аппаратов.

В хим технологии объекты описываются нелинейными ур-ями. Для упрощения расчетов проводят операцию-линериализацию - замена нелинейных функциональных зависимостей на линейную опред. интервале входной величины.

Динамические х-ки - уравнения устанавливающие зависимость изменения в времени выходной величины от вариации входных возникающих параметров.

Универсальный видом описания динамических х-к является диф. уравнение.

Переходный процесс - переход из одного установленного состояния в другое.

Для определения динам. х-к и возможности сравнения их друг с другом применяют тепловые законы изменения тепловых параметров. Если величина теплового сигнала равна 1 тогда наз. Единичный скачок.

Временная х-ка – это отклик объекта на входной импульс.

26. Интерпритация уравнений регрессии

Интерпритация ур-ния регрессии включают анализ влияния ф-ров и их взаимодействия, а также особ-сти поведения отклика в различных частях изучаемой области факторного пространства. Влияние факт прежде всего анализир по ур-нению первой степени.В таком случае вначале оценивают знак коэф.регрессии,показывает в какую сторону уменьшится или увеличится влияние на отклик данный фактор. Для того чтобы интерпретировать коэф. уравнения при регрессии взаимодей факторов:

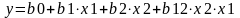
Если задать опред.значение факторов х2,тогда оно перейдет в др.фактор х1.При х1=-1

При х2=0

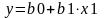
При х2=1

Если b12=0 тогда в уравнении при коэф. Х1 одинаковые, т.е.сила влияния фактора х1 не зависит от влияния х2.Если знаки при b1,b12 одинаковые тогда х1 влияет сильнее чем х2.Если знаки разные ,то х1 ослабевает с увелич х2.

В том случае если оба коэф. b1,b2,а также в12 имеют один. Знак обычно говорят о влиянии х1 и х2.

Если объем ур. 2-ой степени тогда чаще всего при его интерпритации представл. Интерес положения экстремума. Для а) можно найти точку оптимизма ,а график позволяет оценить поведение отклика вблизи ее б) поверхн отклика повыш. В сторону увелич х1и уменьшен.х2 Для поиска максимума отклика необходимо двигаться в сторону .В случае б)экстремума нет,а есть седло –точка движения от которой в любом направлении вдоль данной прямой Если факторов больше чем 2,тогда график аналогичен.