23. Критерий исключения грубой ошибки.

Часто возникает вопрос о том, следует ли отвергать некоторые результаты эксперимента, резко отличающиеся от остальных. Если эти результаты получены из-за грубой ошибки, то их необходимо отбросить, не подвергая никаким статистическим оценкам. В противном случае необходимо произвести проверку резко выделяющихся значений.

П оэтому нуль-гипотеза имеет вид: подозрительный результат относится к той же генеральной совокупности, что и остальные. Альтернативная: этот результат порожден грубой ошибкой и должен быть исключен из дальнейшей обработки данных.

Критерий проверки r имеет вид

где x_под – «подозрительный» результат (наибольший или наименьший);

– среднее, полученное по формуле;

S – среднеквадратичное отклонение; при этом в расчет х и S включается «подозрительный» результат;

n – количество измерений.

Полученное значение критерия сравнивают с табличным, полученным при заданных значениях уровня значимости α и числа степеней свободы v=n-1. Если полученное значение r больше значения, соответствующего табличному r_кр при данном n с заданным уровнем значимости, например, 0,05, то исследуемое наблюдение следует отбросить, если r< r_кр, то его следует оставить.

Критерий Фишера F. Прежде чем сравнивать средние значения двух выборок, необходимо убедиться в равенстве их дисперсий. При нормальном законе распределения СВ для проверки гипотезы о равенстве (однородности) выборочных дисперсий в качестве критерия используется статистика, которая равна отношению двух независимых оценок дисперсий генеральной совокупност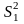и и , имеющих степень свободы соответственно v₁ и v₂, т.е.

При этом должно выполняться условие 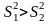, где – большая величина выборочной дисперсии в двух выборках.

Найденное значение сравнивается с табличным при заданном уровне значимости p и степенях свободы v₁=n₁–1 и v₂=n₂-1. Если F<F_кр, тогда гипотеза о равенстве выборочных дисперсий принимается. Критерий Стьюдента t. Для проверки гипотезы о равенстве двух выборочных средних значений СВ, имеющей нормальный закон распределения, используют критерий Стьюдента t.

Нуль-гипотеза здесь: средние значения в двух сериях измерений являются оценками одного и того же генерального значения (математического ожидания, истинного значения).

Если серии измерений, в которых получены средние, сделаны с разной точностью (с разными дисперсиями), то процедура сравнения средних резко усложняется. В этих случаях можно рекомендовать специальные методы. Если дисперсии однородны и найдена общая оценка, тогда проверка проводится по критерию Стьюдента

где п₁ и n₂ – числа измерений в первой и второй сериях; s – единая оценка стандартного отклонения по всей совокупности измерений.

Критическое значение t зависит от v и α.

24. Планы второго порядка. Центральные композиционные планы.Статистический анализ уравнения регрессии для планов второго порядка.

Область близкую к экстремуму функции отклика (область оптимума) называют почти стационарной областью. Для описания этой области применяют полиномы вида

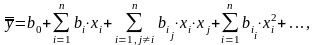
при этом количество необходимых опытов резко увеличивается при возрастании числа членов аппроксимирующего полинома.

В этой связи, имеются хорошо разработанные планы второго порядка, например центральное композиционное ротатабельное планирование (ЦКРП).

Центральным план называют вследствие симметричности относительно центра плана (точки, в которой все кодированные факторы x_u равны нулю); композиционным – потому, что они компонуются путем добавления определенного числа опытов к плану 1-го порядка, например плану ПФЭ.

α – звездное плечо.

Рисунок – Расположение опытных точек в плане 2-го порядка

При построении ЦКП к точкам плана ПФЭ добавляются точки в центре плана (центральные точки – одна или несколько параллельных) и точки, расположенные на всех осях координат на одинаковых расстояниях ±α от центра (звездные точки). Величину α называют звездным плечом. Для разных вариантов планов звездное плечо может быть разным.

Д ля двух факторов матрица такого плана имеет вид:

Планы второго порядка в строгом смысле не ортогональны. Специальный подбор величины α и добавочное преобразование переменных позволяют получить ортогональность и избавиться от взаимной корреляции коэффициентов при квадратах факторов.

Дисперсию воспроизводимости определяют по опытам в центре плана:

где y_0u – значения отклика, полученное по опытам в центре плана, – среднее значение отклика, полученное в центре плана; n₀ – число нулевых точек; v₀ – число степеней свободы дисперсии воспроизводимости.

Для проверки значимости коэффициентов регрессии вычисляют:

1) дисперсию коэффициентов уравнения регрессии по следующим формулам:

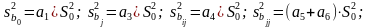
где a₁, a₃, a₄, a₅, a₆ – значения констант, согласно справочным данным (см. приложение);

2) составляют отношения

здесь

и сравнивают их со значением t-критерия, которое находят по таблицам распределения Стьюдента для выбранного уровня значимости p (например, p =0,05) и числа степеней свободы v=v₀, то есть

Если условие выполняется, то проверяемый коэффициент регрессии значим и, наоборот. Если один из квадратичных эффектов оказался незначимым, после его исключения следует пересчитать уравнение регрессии.

Проверку адекватности уравнения регрессии проводят по критерию Фишера:

где – дисперсия адекватности, которая определяется из соотношения:

число степеней свободы дисперсии адекватности

Остаточную дисперсию рассчитывают по формуле:

где 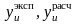– экспериментальные и расчетные согласно модели значения отклика; N – количество опытов; l – число значимых коэффициентов в уравнении регрессии. Уравнение адекватно, если F<F_кр. F_кр – табличное значение критерия Фишера для выбранного уровня значимости и числа степеней свободы числителя v_ад=v₁ и знаменателя v₀=v₂.