21. Математическое описание химико-технологических систем при детерминированном подходе. Иерархическая структура математической модели.

Детерминированный подход к построению моделей базируется на изучении физической сущности и анализе механизма процесса, наличии сведений о физической природе моделируемого объекта и известных основных теоретических закономерностях протекающего в нём процесса.

При этом моделировании в состав математического описания вводятся зависимости связывающие параметры характеризующие изучаемый объект в единую систему уравнений, это могут быть выражения, отражающие фундаментальные законы сохранения вещества и энергии, уравнения описывающие физические и химические(элементарные) процессы, протекающие в моделируемой системе. Кроме того в состав математического описания могут входить эмпирические или полуэмпирические зависимости между некоторыми параметрами теоретическая форма которых неизвестна или очень сложна. Также в состав математического описания вводят ограничения на некоторые параметры.

Преимущества: 1)качественно более правильно характеризует моделируемый объект даже при наличии недостаточно точных в количественном отношении параметров модели; 2) с помощью этих моделей можно изучать общие свойства объектов моделирования, относящихся к определённому классу.

Недостатки: составление таких моделей требуют по сравнению со статистическими больших затрат времени и средств.

Блок – схема состава математического описания при детерменированном подходе в общем виде.

Общие материальные и энергетические балансы

О бщие закономерности, зако- Математическое Теоретические и мерности элементарных ожидание эмпирические

закономерности

процессов

Ограничения на переменные параметры объекта

Для составления модели детерминированным способом начинается с разделения технологического процесса на отдельные(элементарные) составные части, отражающие свойства какого-либо одного класса явления (химическое превращение, массаобмен, теплообмен, гидродинамические и механические процессы.

22. Проверак значимости коэффициентов регрессии и адекватности статистической модели, полученной при дфэ.

Общая последовательность анализа экспериментальных данных:

1. Построить матрицу планирования ДФЭ 2^4-1 в некодированных и кодированных величинах.

2. Для приведенных экспериментальных данных рассчитать коэффициенты регрессии линейного полинома.

3. Проверить однородность выборочных дисперсий по критерию Кохрена.

4. Рассчитать дисперсию воспроизводимости.

5. Определить значимость коэффициентов регрессии.

6. Проверить адекватность статистической модели, используя результаты проведенных параллельных опытов.

Если в дополнение к столбцам x₁, x₂, x₃ вычислить столбцы для взаимодействий, то окажется (матрица I) столбец х₁ совпадает со столбцом х₂, столбец х₂ – со столбцом х₁х₃, столбец х₁х₂х₃ со столбцом х₀ х₃ (столбцы х₁х₃, x₂x₃, х₁х₂х₃ введены в матрицу ДФЭ 2^3-1 для пояснения).

Таким образом, сокращение числа опытов приводит к появлению корреляции между некоторыми столбцами матрицы планирования, что не позволяет раздельно оценивать эффекты факторов и эффекты взаимодействия, и, следовательно, оценки получаются смешанными (оценки в которых учитываются линейные эффекты и эффекты взаимодействия).

По данному плану (матрица I) можно выразить коэффициенты

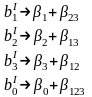
где буквами греческого алфавита обозначены коэффициенты регрессии генеральной совокупности (математические ожидания соответствующих коэффициентов), а буквами латинского алфавита – их оценки. Можно реализовать и другую полуреплику, где х₃ = –х₁х₂ (матрица II, таблица).

По матрице II смешанные оценки коэффициентов регрессии будут

В процедуру проверки значимости коэффициентов регрессии входит:

а) вычисление дисперсий коэффициентов регрессии , которые при факторном планировании первого порядка для всех коэффициентов регрессии равны и минимальны, по формуле:

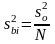
где N – число опытов в матрице планирования;

б) составление отношений:

здесь

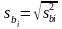
и сравнение их со значением t-критерия, которое находят по таблицам распределения Стьюдента для выбранного уровня значимости p (например, p =0,05) и числа степеней свободы v=N^*·(m–1), то есть

Если условие выполняется, то проверяемый коэффициент регрессии значимый и, наоборот.

В практических расчетах для проверки значимости коэффициентов b_i наиболее часто используют следующие выражения:

где b_i – доверительный интервал для коэффициента – тот интервал, в пределах которого коэффициент, в действительности равный нулю, может отклониться от истинного значения c заданной малой вероятностью;

t – находят по таблицам критерия Стьюдента для выбранного уровня значимости и числа степеней свободы v=N^*.

Если его абсолютное значение коэффициента регрессии превышает величину абсолютного значения отклонения , тогда коэффициент регрессии значим.

Чтобы проверить гипотезу об адекватности математической модели используют критерий Фишера:

Остаточная дисперсия вычисляется по формуле:

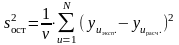
где v=(N–l–1) – число степеней свободы; N – количество опытов (число строк в матрице плана); l – число значимых коэффициентов регрессии.

где F_кр – критическое значение критерия Фишера для выбранного уровня значимости (p=0,05) и степеней свободы числителя v₁=N–l–1 и знаменателя v₂=N^*(т–1), N^* – количество групп параллельных опытов.

При соблюдении условия считают, что полученное уравнение регрессии адекватно.