2.4.1. Метод рабочих характеристик

Метод рабочих характеристик состоит в следующем:

Все показатели качества, кроме одного, которому присваивается первый номер, переводятся в разряд ограничений типа равенств и ищется минимум (по всем строго допустимым системам) показателя k₁, т.е. решается задача:

Обеспечить _min k₁ при k₂= k₂ , k₃= k₃,…, k_m= k_m . (2.21)

S М_сд

Здесь и далее обозначение S М_сд означает, что рассматриваются лишь те варианты построения системы, которые удовлетворяют исходным данным Д", в частности ограничениям О_s структуры и параметров системы и ограничениям О_к показателей качества k₁,…k_m (см. соотн. 2.11).

Пусть результатом решения задачи (2.21) является некоторая система (класс систем) S_p, а соответствующее ей минимальное значение показателя k₁ равно k_1min. Очевидно, результаты решения задачи (2.21) т.е. вид системы S_p и значение величины k_1min будут в общем случае зависеть от фиксированных значений k₂,…k_m показателей качества, переведённых в разряд ограничений типа равенств, т.е.

S_p= S_p (k₂…k_m ), (2.22)

K_1min= f_p (k₂,...,k_m ), (2.23)

Пример 1.

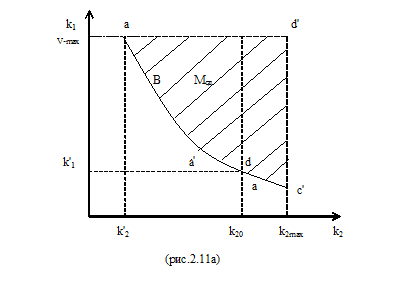
Рисунок 2.11а

Пусть множество М_сд имеет вид, изображённый на рисунке 2.11а, причём, как уже было показано, множество М_нx есть совокупность точек левой нижней границы a'b c', в соответствии с методом рабочих характеристик. В соответствии с этим методом должна решаться задача:

Обеспечить min k₁ при k₂= k₂

S М_сд

При всех допустимых значениях показателя k₂.

Из ограничения k₂≤ k_2max следует, что и k₂≤ k_2max; из ограничения же k₁≤ k_1max, следует, что k₂ k₂. Пусть, например, в этой области выбрано k₂= k₂₀.Из рисунка 2.11а видно, что при таком значении k₂ минимально возможное значение показателя k₁ равно k'₁ и ему соответствует точка d на левой нижней границе области М_сд. Таким образом находится точка d искомого множества М_нх. Решая эту задачу последовательно для всех допустимых неравенством

k'₂≤ k₂≤ k_2max

значений показателя k₂, находим тем самым все точки левой нижней границы a'bc'd', т.е. всё множество М_нх. Зависимость k_1min=fp(k₂) в данном случае оказалась монотонно убывающей, что говорит о совпадении М_р и М_нх.

Где fp (k₂,…, k_m)- некоторая функция показателей k₂,…k_m, которую будем называть рабочей поверхностью.

Зависимости (2.22) и (2.23) можно найти, варьируя значения показателей k₂,…k_m в допустимых для них ограничениями (2.10) пределах.

Доказано, что необходимым и достаточным условием совпадения рабочей поверхности fp(k₁,…k_m) с диаграммой обмена (2.20), т.е. нахождение необходимого М_нх, является монотонно убывающий характер функции (2.23) по каждому из её аргументов. Если же рабочая поверхность не обладает указанным свойством строгой монотонности, то она также содержит все точки множества М_нх, но, кроме того, в ней имеются и худшие точки.

Пример 2. Граница abc множества М_сд не является монотонно убывающей (рисунок 2.11б)

К₁

k₁=fp(k₂) a d

М_сд

B c

К₂

Рисунок 2.11б.

Множество М_нх содержит лишь точки, расположенные на участке кривой ab (любая из точек участка bc, не совпадающая с b, является худшей, так как ей соответствует большее значение показателя k₂ при том же значении показателя k₁).

Таким образом, метод рабочих характеристик сводится к следующим этапам:

1. Все показатели качества, кроме одного (k₁), переводятся в разряд ограничений типа равенств, т.е. формулируется задача (2.21)

2. Задача (2.21) решается последовательно для всех допустимых ограничениями (2.10) комбинаций (k₁,…k_m) показателей качества, переведённых в разряд ограничений, в результате чего, находится рабочая поверхность(2.23).

3. Если зависимость (2.23) оказывается монотонно убывающей по каждому из её аргументов, то она полностью совпадает с исходной диаграммой обмена, геометрическим методом всех точек множества М_нх. В противном случае, из найденного множества точек необходимо исключить худшие.