19. Условия коллинеарности, ортогональности и комплонарности векторов

1) Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. Условия компланарности векторов:

• Три вектора компланарны если их смешанное произведение равно нулю.

• Три вектора компланарны если они линейно зависимы.

2) Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными.

Условия коллинеарности векторов

• Два вектора коллинеарные, если отношения их координат равны.

• Два вектора коллинеарные, если их векторное произведение равно нулю.

3) Условия ортогональности векторов. Два вектора a и b

 ортогональны (перпендикулярны), если их скалярное произведение равно нулю

a· b = 0

20. Деление отрезка в заданном отношении

1. Если x₁ и y₁ - координаты точки A, а x₂ и y₂ - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении  , определяются по формулам

Если  , то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам

21. Прямая линия на плоскости: уравнение прямой с угловым коэффициентом; уравнение прямой, проходящей через две данные точки; уравнение прямой, проходящей через данную точку в заданном направлении; уравнение прямой в отрезках

уравнение прямой с угловым коэффициентом:

у=kx+b: k = tgф - угловой коэффициент

уравнение прямой, проходящей через две данные точки:

уравнение прямой, проходящей через данную точку в заданном направлении:

y-y0=k(x-x0)

уравнение прямой в отрезках:

22. Общее уравнение прямой на плоскости

Общее уравнение прямой:

Ax+By+C=0 , где A2+B2 не равно 0

23. Каноническое, нормальное, параметричекие уравнения прямой

Нормальное: 

Каноническое:

где   — координаты   и   направляющего вектора прямой,   и   координаты точки, принадлежащей прямой.

Параметрические:

где   — производный параметр,   — координаты   и   направляющего вектора прямой

24. Угол между прямыми. Условия параллельности и перпендикулярности двух прямых

Углом между прямыми в пространстве называют любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Угол между прямыми в пространстве равен углу между их направляющими векторами  . Поэтому, если две прямые заданы каноническими уравнениями вида   и   то косинус угла между ними можно найти по формуле:

).

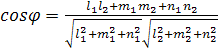Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов  .

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны:

 – условие параллельности прямых.

 

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:

 – условие перпендикулярности прямых.

25. Общее уравнение плоскости

можно записать в виде  , приняв  , получаем общее уравнение плоскости:

26. Уравнения плоскости: проходящей через три точки; уравнение плоскости в отрезках; нормальное уравнение

Уравнение плоскости, проходящей через три данные точки

Пусть плоскость проходит через точки   и  , не лежащие на одной прямой и   – произвольная точка плоскости. Тогда векторы  ,

  ,   компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем:

.

 

Это уравнение, которому удовлетворяют координаты   любой точки, лежащей на искомой плоскости, является уравнением плоскости, проходящей через три данные точки.

Нормальное уравнение плоскости

Положение плоскости   вполне определяется заданием единичного вектора  , имеющего направление перпендикуляра  , опущенного на плоскость из начала координат, и длиной p этого перпендикуляра

Пусть  , а   – углы, образованные единичным вектором   с осями   и  ;   Возьмем на плоскости произвольную точку   и соединим ее с началом координат. Образуем вектор  . При любом положении точки Μ на плоскости   проекция радиус-вектора   на направление вектора   всегда равно  :  , т.е.   или   – нормальное уравнение плоскости в векторной форме. Записав его в координатах получим нормальное уравнение плоскости в координатной форме:

 

.

27. Условия параллельности, перпендикулярности и совпадения плоскостей

Условие параллельности плоскостейзаключается в параллельности нормалей  , а условие перпендикулярности плоскостей – в перпендикулярности нормалей  или равенстве нулю их скалярного произведения:  Для нахождения острого угла следует взять модуль правой части .Если плоскости   и   перпендикулярны, то таковы же их нормали,  т. е.   и наоборот

28. Эллипс, его определение, уравнение

 Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная

   где 

29. Гипербола, его определение, уравнение.

 Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная

гипербола в выбранной выше системе координат имеет уравнение    где

30. Парабола, ее определение, уравнение.

Параболой ( рис.1 ) называется геометрическое место точек, равноудалённых  от заданной точки  F , называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.

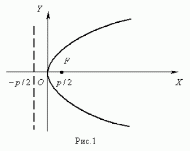
Уравнение параболы ( рис.1 ) :

 

y ² = 2 p x .

 

Здесь ось ОХ  является осью симметрии параболы.

 

Пусть  Р ( х₁ ,  у ₁ ) – точка параболы, тогда  уравнение касательной к параболе  в данной точке имеет вид:

 

у ₁ y  = p ( x +  х₁ ) .          

 

Условие касания прямой  y = m x + k  и параболы  y ² = 2 p x :

 

2 m k   = p .