Возведение в степень комплексных чисел
Операцию возведения в степень удобнее выполнять, когда комплексное число записано в тригонометрической или впоказательной форме.
INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2429.gif" \* MERGEFORMATINET
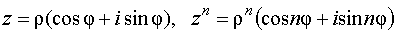,INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2430.gif" \* MERGEFORMATINET
.
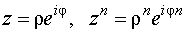Для возведения комплексного числа в степень нужно модуль возвысить в эту степень, а аргумент умножить на показатель степени.
Извлечение корня
Определение. Корнем n -ой степени из комплексного числа называется такое комплексное число, n -я степень которого равна подкоренному числу.
Из этого
определения следует, что из равенства
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2431.gif"
\* MERGEFORMATINET
следует
равенство
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2432.gif"
\* MERGEFORMATINET
.
Из равенства
комплексных чисел следует
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2434.gif"
\* MERGEFORMATINET
,
а аргументы отличаются на число, кратное
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2433.gif"
\* MERGEFORMATINET
;
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2435.gif"
\* MERGEFORMATINET
.
Отсюда
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2436.gif"
\* MERGEFORMATINET
,
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2437.gif"
\* MERGEFORMATINET
.
Здесь
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2438.gif"
\* MERGEFORMATINET
есть
арифметическое значение корня,
а k – любое
целое число. Таким образом, получается
формула
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2439.gif"
\* MERGEFORMATINET
.
В этой формуле число k может принимать всевозможные целые значения, но различных значений корня будет только n и они соответствуют значениям k = 0, 1, 2, … , n - 1.
Докажем
этот факт. Действительно, правые части
в этой формуле различны тогда, когда
аргументы
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2440.gif"
\* MERGEFORMATINET
и
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2441.gif"
\* MERGEFORMATINET
отличаются
на величину, не кратную
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2433.gif"
\* MERGEFORMATINET
, и
будут одинаковыми, если указанные
аргументы отличаются на величину,
кратную
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2433.gif"
\* MERGEFORMATINET
.
Поэтому разность
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2442.gif"
\* MERGEFORMATINET
не может быть кратна INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2433.gif" \* MERGEFORMATINET . Из этого результата и следует, что любым подряд взятым n целым числам k соответствуют n различных значений корня.
Пусть
теперь k3–
целое число, не входящее в эту
последовательность подряд взятых
значений k . Это число можно представить
в видеk3= gn + ki,
где g –
целое число, а ki –
одно из чисел этого ряда, поэтому
INCLUDEPICTURE
"http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2443.gif"
\* MERGEFORMATINET
,
то есть значению k3соответствует
то же значение корня, что и значению ki.
Вывод: корень n -ой степени из комплексного числа имеет n различных значений. Исключением из этого правила является лишь частный случай, когда извлекается корень из нуля. В этом случае все значения корня равны нулю.
f = f(x) = a0 + a1x