Умножение комплексных чисел

        Определение. Произведением двух комплексных чисел называется такое комплексное число, модуль которого равен произведению  модулей сомножителей, а аргумент –  сумме аргументов сомножителей.

        Это определение совершенно очевидно, если использовать показательную форму комплексного числа:

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2412.gif" \* MERGEFORMATINET

        Пусть комплексные числа даны в алгебраической форме. Найдём их произведение: (a₁ + b₁i) (a₂ + b₂i ) = x + iy.

Имеем  INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2413.gif" \* MERGEFORMATINET .

Согласно определению умножения можем записать:

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2414.gif" \* MERGEFORMATINET .

Распишем:       INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2415.gif" \* MERGEFORMATINET ,

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2416.gif" \* MERGEFORMATINET

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2417.gif" \* MERGEFORMATINET

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2418.gif" \* MERGEFORMATINET ,

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2419.gif" \* MERGEFORMATINET

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2420.gif" \* MERGEFORMATINET .

Окончательно получим:

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2421.gif" \* MERGEFORMATINET .

        Отсюда следует правило умножения комплексных чисел в алгебраической форме: комплексные числа можно перемножать как многочлены.

        Если  z  = а + b i  –  комплексное число, то число  INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2422.gif" \* MERGEFORMATINET  называется сопряжённым с числом z . Его обозначают при помощи черты над числом.

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2423.gif" \* MERGEFORMATINET , но  INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2425.gif" \* MERGEFORMATINET , следовательно,  INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2424.gif" \* MERGEFORMATINET .

Деление комплексных чисел

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2426.gif" \* MERGEFORMATINET .

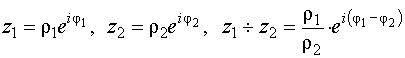Модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.

Если делимое и делитель даны в алгебраической форме, то правило деления таково: для того, чтобы разделить комплексное число(a₁ + b₁i )  на другое комплексное число  (a₂ + b₂i ), то есть найти  INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2427.gif" \* MERGEFORMATINET 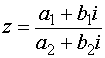, нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.

INCLUDEPICTURE "http://kurs.ido.tpu.ru/courses/ingmathsem2/tema21_2/Image2428.gif" \* MERGEFORMATINET .

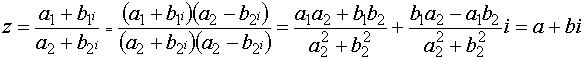        В результате операции получили элемент того же множества. Значит, операция деления считается введённой.