Изобарная теплоемкость

В процессе v = const теплота, сооб­щаемая газу, идет лишь на изменение его внутренней энергии, тогда как в про­цессе р = const теплота расходуется и на увеличение внутренней энергии и на со­вершение работы против внешних сил. Поэтому с_р больше c_v на величину этой работы. Из уравнения (4') при р = const имеем:

δq_p = (_{ди/ дТ})_V · dT_p + [ р + (_{ди / дυ})т ] • d_{υ P} (9)

Изобарная теплоёмкость с_р равна отношению количество теплоты δq_p в процессе при р = const к изменению температуры тела dТ_p

с_р = δq_p/dT_p (10) Учитывая выражение (9) можно записать:

Ср = (_{ди/ дТ})v + [ р + (_{ди / дυ})т ] • (_дυ/dT)р

_{Используя уравнение (6}^’_{) запишем:}

c_p = c_v + [ р + (_{ди / дυ})т ] • (_дυ/dT)р (11)

Для идеального газа. (_дu / _дv)_T= 0, а так как R = р · v I T, то дифференцируя его при р = const, имеем:

R = p · (dυ/dT)p, (12)

Подставляя (12) в (11) имеем окончательно:

с_р = c_v + R (13) Выражение (13) носит название уравнения Майера. Для реальных газов

^с_р ^{- c}_v ^{> R, так как при расширении (при р = const) совершается не только} внешняя, но и внутренняя работа, связанная с изменением внутренней потенциальной энергией газа, что вызывает больший расход теплоты.

Соотношение между теплоёмкостями определяется равенством

c_р = c_v + R . (13)

Выражение (13) носит название уравнения Майера. Роберт Ю. Майер был вюртембергским врачом, открытие им уравнения (13) (или принципа эквивалентности) относится к 1842 году.

В термодинамике часто используется отношение теплоёмкостей:

с_р / c_v = с_p’/с_v’= (µc_p)/(µc_v) = k; k = c_p/c_v = (c_v + R)/c_v ⁼ 1+R/c_v, где k - показатель адиабаты.

Для идеальных газов k зависит от температуры. Методом статистической термодинамики установлено, что одноатомные газы имеют k = 1,66, двухатомные k = 1,4, трёхатомные к = 1,33, перегретый водяной пар к = 1,3.

2.2. Истинная и средняя теплоёмкости.

Теплоемкость реального газа очень слабо зависит давления. Поскольку теплоемкость реального газа, в основном, зависит от температуры, в термодинамике различают истинную и среднюю теплоемкости.

Для уяснения методики определения сред­ней теплоемкости по указанным таблицам вос­пользуемся рис. 2. Истинной теплоёмкости соответствует кривая 3, определяемая зависимостью c = f(t). Заштрихованная под ней пло­щадь эквивалентна количеству теплоты q, необходимому для нагревания 1 кг рабочего тела от температуры t₁ до t₂ :

.

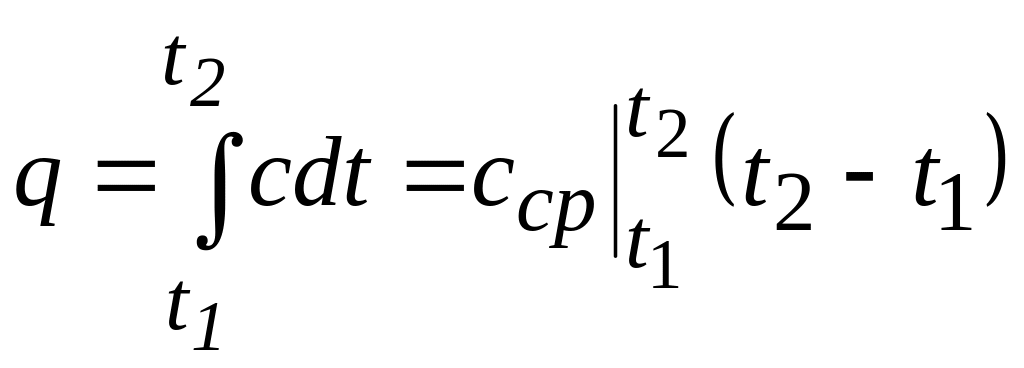Ее можно заменить равновеликим прямоугольником с основанием t₂ - t₁ и высотой, численно равной средней теплоемкости. Обозначается средняя теплоёмкость символом .

Рис. 2. Зависимость истинной теплоемкости от температуры

Средней теплоемкостью данного процесса в интер­вале температур от t₁ до t₂ называется отношение количества тепло­ты q , сообщаемой газу в данном интервале температур, к разности конечной и начальной температур:

.

Для практических расчётов теплоем­кости всех веществ сводят в таблицы, причем с целью сокращения объема таб­лиц средние теплоемкости приводят в них для интервала температур от 0 ⁰С до t ⁰С .

Если необходимо с помощью таблиц определить среднюю теплоёмкость в интервале t₂ - t₁, то

.

Все изложенное относится к массовым, мольным и объемным теплоемкостям.