8.Средние величина простая

Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности.

Величина средней дает обобщающую количественную характеристику всей совокупности и характеризует ее в отношении данного признака.

Так, например, средняя заработная плата дает обобщающую количественную характеристику состояния оплаты труда рассматриваемой совокупности работников. Кроме того, используя средние величины, имеется возможность сопоставлять различные информационные совокупности. Так, например, можно сравнивать различные организации по уровню производительности труда, а также по уровню фондоотдачи, материалоотдачи и по другим показателям.

Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором.

9.Средние величина взвешенная

Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют  статистическим весом или весом средней.

10.Свойства средней арифметической величины

Свойство первое (нулевое): сумма положительных отклонений индивидуальных значений признака от его среднего значения равна сумме отрицательных отклонений. Это очень важное свойство, поскольку оно показывает, что любые отклонения (как с +, так и с -), вызванные случайными причинами, взаимно будут погашены.

Доказательство:

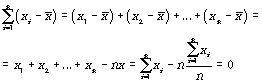
Свойство второе (минимальное): сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа (а), т.е. есть число минимальное.

Доказательство.

Составим сумму квадратов отклонений от переменной а:

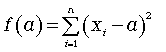 (5.4)

Чтобы найти экстремум этой функции, необходимо ее производную по а приравнять нулю:

Отсюда получаем:

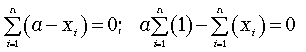
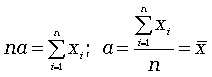 (5.5)

Следовательно, экстремум суммы квадратов отклонений достигается при  . Этот экстремум - минимум, так как функция не может иметь максимума.

Свойство третье: средняя арифметическая постоянной величины равна этой постоянной:   при а = const.

Кроме этих трех важнейших свойств средней арифметической существуют так называемые расчетные свойства, которые постепенно теряют свою значимость в связи с использованием электронно-вычислительной техники:

• если индивидуальное значение признака каждой единицы умножить или разделить на постоянное число, то средняя арифметическая увеличится или уменьшится во столько же раз;

• средняя арифметическая не изменится, если вес (частоту) каждого значения признака разделить на постоянное число;

• если индивидуальные значения признака каждой единицы уменьшить или увеличить на одну и ту же величину, то средняя арифметическая уменьшится или увеличится на ту же самую величину.

11.Построение ряда распределения

Изучение структуры той или иной совокупности достигается по­строением рядов распределения,характеризующих распреде­ление единиц совокупности по одному признаку.

Ряды распределения делятся на вариационные и атрибутивные. Вариационный ряд — это распределение единиц сово­купности по количественному признаку. В атрибутивных ря­дахпредставлена группировка по атрибутивным (качественным) признакам.

Форма построения вариационного ряда зависит от характера изменения изучаемого признака, он может быть построен в форме дискретного ряда или в форме интервального ряда.

По характеру вариации значений признака различают:

• признаки с прерывным изменением (дискретные);

• признаки с непрерывным изменением (непрерывные).

Признаки с прерывным изменением могут принимать лишь конечное число определенных значений (например, тариф­ный разряд работников, число туристов в группе и др.). Признаки с непрерывным изменением могут принимать в определен­ных границах любые значения (например, стаж работы, размер дохода и т. д.).