1. Примеры решения типовых задач: прямая на плоскости

Задача 2.1

Составить общее уравнение прямой, проходящей через точки (1,2) и (-2,3).

Решение: Обозначим точки соответственно и ; согласно формуле ( 2.0 ) имеем: . Избавимся от дроби: . Раскрыв скобки и перенеся все члены в одну сторону, получаем: . Ответ: .

Задача 2.2

Составить уравнение прямой, проходящей через точку параллельно прямой .

Решение: Так как искомая прямая по условию задачи должна быть параллельной исходной, это значит, что они имеют один угол наклона к оси . Угол наклона исходной прямой можно определить из формулы ( 2.0 ): . Исходная прямая задана в общей форме, следовательно для нее ; ; подставляя значения коэффициентов исходной прямой, находим . Обозначим координаты точки как , имеем , ; прямую, проходящую через эту точку, можно описать уравнением с угловым коэффициентом ( 2.0 ); подставим в него известные значения, получим: . Проведя несложные преобразования, получим искомое уравнение: .

Замечание: можно было провести и другие рассуждения:

1. Прямые должны быть параллельны, это значит, первые два коэффициента в уравнении у них должны быть одинаковы ( – имеет одно значение), следовательно, нужно найти только значение свободного члена ; по определению , где – известны из исходного уравнения: ; , а – координаты начального радиус-вектора.

2. Нормаль у параллельных прямых – общая, значит, начальный радиус-вектор можно провести через заданную точку : ; подставив ее координаты в выражение для , получаем: .

3. Подставляем в искомое уравнение, получаем искомое уравнение.

Ответ: .

Задача 2.3

Составить уравнение прямой, проходящей через точку перпендикулярно прямой .

Решение: Искомая прямая является нормалью к заданной прямой, поэтому для решения можно использовать уравнение в канонической форме (формула ( 2.0 )). В формуле: – координаты направляющего вектора исходной прямой, в нашем случае они совпадают по значению с коэффициентами из исходного уравнения: ; . – координаты заданной точки, то есть ; . Подставляя значения в формулу ( 2.0 ), получаем: . Решая данное уравнение, получаем ответ. Ответ: .

Задача 2.4

Две стороны квадрата лежат на прямых и . Вычислить его площадь.

Решение: Из заданных уравнений прямых следует, что они параллельны (коэффициенты и – одинаковы). Для нахождения длины стороны квадрата нужно найти расстояние от одной прямой до другой. Это можно сделать, взяв точку на одной прямой и определить расстояние от нее до другой прямой. Возьмем первую прямую: , пусть , подставив это значение в уравнение, получим уравнение относительно , откуда найдем . Таким образом, получим точку, принадлежащую первой прямой: .

Расстояние от точки с известными координатами до прямой определяем с помощью формулы ( 2.0 ): .

Теперь определяем площадь: . Ответ: .

Задача 2.5

По известным координатам вершин треугольника , , записать для его сторон уравнения в общем виде и уравнение в общем виде биссектрисы угла .

Решение: Так как нам известны координаты вершин, то проще всего получить уравнение стороны в канонической форме – формула ( 2.0 ), от которого легко перейти к уравнению в общей форме. Для канонического уравнения нам нужны координаты точки, принадлежащей стороне и координаты направляющего вектора (параллельного рассматриваемому).

1. Найдем уравнение стороны . В качестве точки прямой можно взять точку с заданными координатами, а в качестве направляющего вектора – вектор . Найдем координаты вектора :

2. Тогда каноническое уравнение стороны запишется как: , или .

3. Аналогично можно получить уравнения остальных сторон треугольника: для стороны : координаты вектора .

4. Откуда каноническое уравнение: . Следовательно, общее уравнение: .

5. Для стороны : координаты направляющего вектора .

6. Каноническое уравнение: , или .

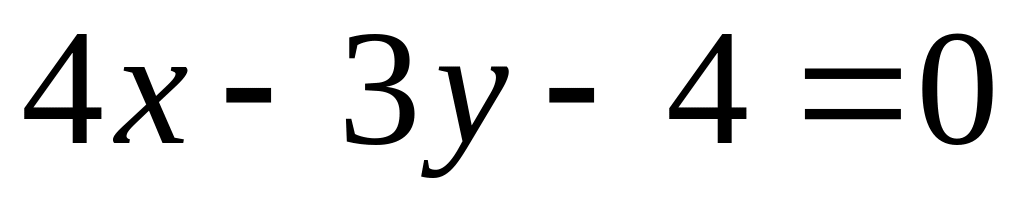7. Выведем общее уравнение для биссектрисы. Известно, что биссектриса делит угол пополам. Если на сторонах и треугольника отложить орты (соответственно и ) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов и ).

8. Для нахождения орта необходимо знать координаты вектора :

, откуда и, соответственно определится как:

(Рис. 2.5).

Рис. 2.5. Иллюстрация решения задачи 2.5

9. Аналогично определим орт :

; ;

. Теперь определим их сумму:

.

10. Тогда каноническое уравнение биссектрисы:

.

Ответ: .