4. Введение в численные методы. Основные понятия

   1. Интерполяция и квадратурные формулы

Интерполирование

Определение 6.1. Пусть функция f (х) задана таблично на [a, b], т.е. задан набор значений: x₀ = a, x_n = b , x₀ < x₁ < x₂ < .... < x_n , y_i = f (x_i) i = 0,..., n

Тогда построение непрерывной на [a, b] функции  (x) , такой что  (x_i) = y_i называется интерполяцией функции f (х) на [a, b].

Определение 6.2. Пусть полином степени n L_n(x) = a₀ xⁿ + a₁ x^n-1 + ... + a_n интерполирует y=f (x) на [a, b], т.е. L_n(x_i) = y_i= f (x_i). Тогда L_n (x) называется интерполяционным полиномом.

Квадратурные формулы

Определение 6.3. Выражение вида , предназначенное для вычисления определенного интеграла называется квадратурной формулой.

Величина R=I  S называется погрешностью квадратурной формулы. Укажем одну их квадратурных формул.

Формула трапеций

Простая : S₁ = (b-a)( f(b) + f(a) )/ 2, R₁ = (b-a)³ f () / 12 ,  (a,b)

Составная: .

Определенный интеграл функции геометрически представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис. 6.1).

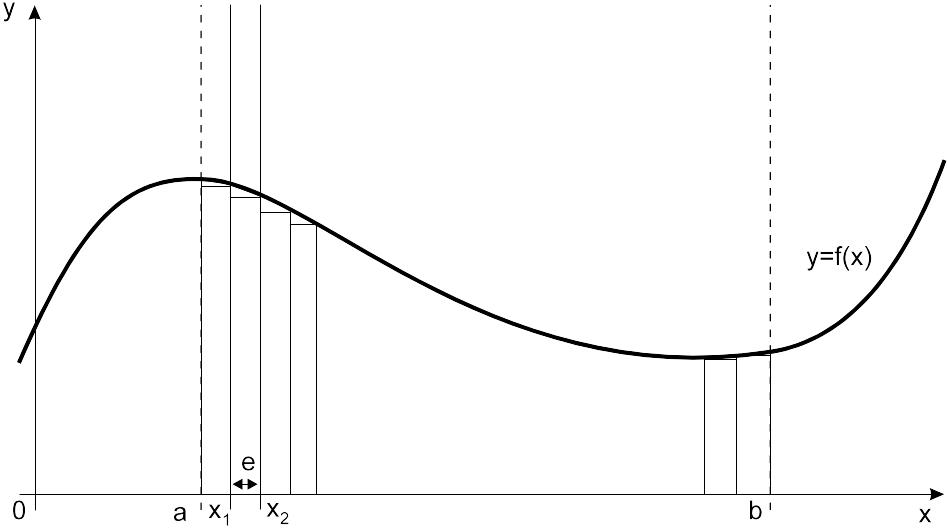
Рис. 6.1. Криволинейная трапеция

Соответственно формуле и составим алгоритм вычисления величины определенного интеграла для таблично заданной функции f(x).

1. Вычисляем .

2. Вычисляем приближенное значение величины определенного интеграла по составной формуле трапеций:

2. Контрольная работа 1. Часть 3.

Для таблично заданной функции (x_i, y_i) = f(x_i), i =0,...,6, решить следующие задачи (далее будем эту функцию обозначать f(x)).

1) Вычислить значение функции f(x) в заданной точке ( x₀, x₆) используя линейную интерполяцию.

2) Вычислить значение функции f(x) в точке ( x₀, x₆) на основе квадратичной интерполяции (используя многочлен Лагранжа второй степени).

3) Вычислить величину определенного интеграла для таблично заданной функции f(x) методом трапеций.

4) Найти наибольшее f_max и наименьшее f_min значения для непрерывной на отрезке [х₀, х₆] функции f (х). Определить точки х_тах и х_min, в которых эти значения достигаются. Задачу решить двумя способами:

а) методом дифференциального исчисления;

b) численным методом золотого сечения. Сравнить результаты двух подходов.

Варианты исходных данных

Вариант 1.

i	0	1	2	3	4	5	6
xi	0.4	0.6	0.8	1.0	1.2	1.4	1.6
yi	3.7	4.8	5.3	5.1	4.9	-0.1	-6.2

=0.44

f (х) = 3.5 x³+6.0 x²  2.3 x + 4.1

Вариант 2.

i	0	1	2	3	4	5	6
xi	0.5	0.7	0.9	1.1	1.3	1.5	1.7
yi	3.7	4.8	5.2	5.0	3.1	-0.2	-7.6

=0.73

f (х) = 2.5 x³+5.0 x²  2.1 x + 3.1

Вариант 3.

i	0	1	2	3	4	5	6
xi	0.5	0.7	0.9	1.1	1.3	1.5	1.7
yi	1.2	3.7	3.3	3.2	2.9	-0.1	-4.2

=1.59

f (х) = 1.5 x³+4.9 x²  2.26 x + 6.1

Вариант 4.

i	0	1	2	3	4	5	6
xi	0.3	0.9	1.5	2.1	2.7	3.3	3.9
yi	2.7	3.7	4.3	4.1	0.1	-1.5	-8.3

=0.47

f (х) = 1.5 x³+3.7 x²  2.56 x + 3.1

Вариант 5.

i	0	1	2	3	4	5	6
xi	0.5	0.8	1.3	1.7	2.1	2.5	2.9
yi	5.3	5.5	6.1	6.3	6.0	-0.3	-2.9

=1.44

f (х) = 1.5 x³+7.0 x²  2.3 x + 4.89

Вариант 6.

i	0	1	2	3	4	5	6
xi	0.2	0.8	1.4	2.0	2.6	3.2	3.8
yi	3.2	4.8	6.3	5.9	4.7	-0.1	-1.1

=0.92

f (х) = 5.1 x³+4.6 x²  2.2 x + 5.1

Вариант 7.

i	0	1	2	3	4	5	6
xi	0.4	0.8	1.2	1.6	2.0	2.4	2.8
yi	4.2	4.3	5.1	4.8	2.7	-0.5	-6.3

=0.86

f (х) = 3.7 x³+6.1 x²  2.25 x + 5.1

Вариант 8.

i	0	1	2	3	4	5	6
xi	0.8	1.2	1.6	2.0	2.4	2.8	3.2
yi	5.1	5.4	6.1	5.8	5.3	0.3	-1.7

=1.73

f (х) = 2.5 x³+5.98 x²  2.01 x + 6.1

Вариант 9.

i	0	1	2	3	4	5	6
xi	0.8	1.1	1.4	1.7	2.0	2.3	2.6
yi	2.3	3.3	5.3	4.7	3.9	-0.5	-4.1

=1.57

f (х) = 2.5 x³+5.8 x²  2.28 x + 4.05

Вариант 10.

i	0	1	2	3	4	5	6
xi	0.4	0.8	1.2	1.6	2.0	2.4	2.8
yi	5.1	5.4	6.1	5.8	0.5	-0.3	-4.2

=2.53

f (х) = 3.47 x³+6.95 x²  3.29 x + 5.05