Контрольная работа 1. Часть 2.
Вариант 2.1
Задание 1.
Выполнить действия с матрицами:
.
Задание 2.
Вычислить определитель матрицы:
.
Задание 3.
Определить, имеет ли матрица
обратную, и, если имеет вычислить ее:
.
Задание 4.
Вычислить ранг матрицы
.
Задание 5. Решить систему уравнений методом Крамера:
.
Задание 6.
Найти общее и одно из частных решений
системы линейных уравнений:
.
Задание 7. Найти общее решение и фундаментальную систему решений:
.
Вариант 2.2
Задание 1.
Выполнить действия с матрицами:
.
Задание 2.
Вычислить определитель матрицы:
.
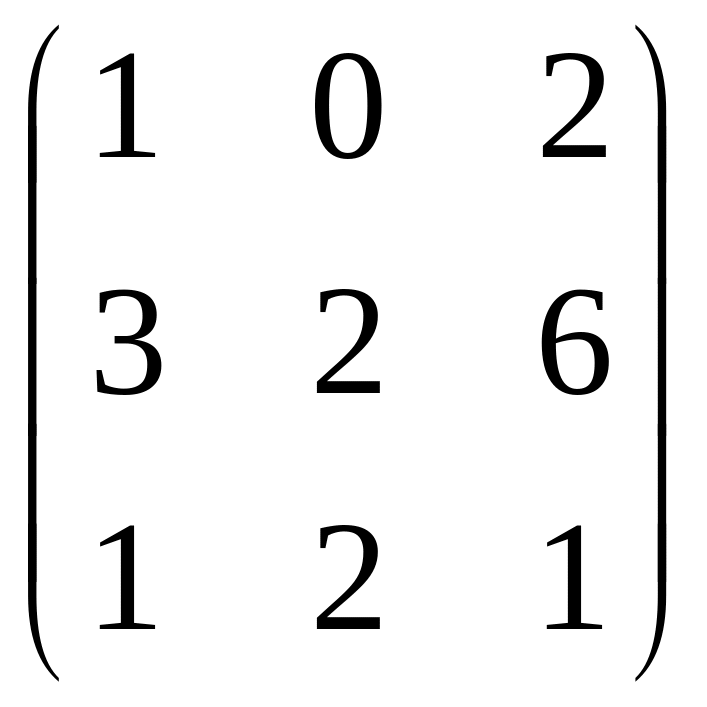Задание 3.
Определить, имеет ли матрица
обратную, и, если имеет вычислить ее:
.
Задание 4.
Вычислить ранг матрицы
.
Задание 5. Решить систему уравнений методом Крамера:
.
Задание 6. Найти общее и одно из частных решений системы линейных уравнений:
.
Задание 7. Найти общее решение и фундаментальную систему решений:
.
Вариант 2.3
Задание 1.
Выполнить действия с матрицами:
.
Задание 2.
Вычислить определитель матрицы:
.
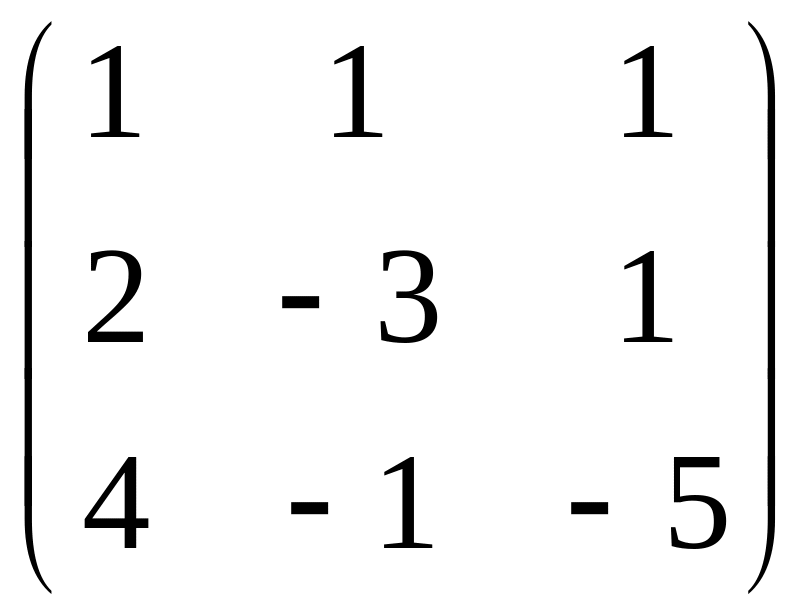Задание 3.
Определить, имеет ли матрица
обратную, и, если имеет вычислить ее:
.
Задание 4.
Вычислить ранг матрицы
.
Задание 5. Решить систему уравнений методом Крамера:
.
Задание 6. Найти общее и одно из частных решений системы линейных уравнений:
.
Задание 7. Найти общее решение и фундаментальную систему решений:
.
Вариант 2.4
Задание 1.
Выполнить действия с матрицами:
.
Задание 2.
Вычислить определитель матрицы:
.
Задание 3.
Определить, имеет ли матрица
обратную, и, если имеет вычислить ее:
.
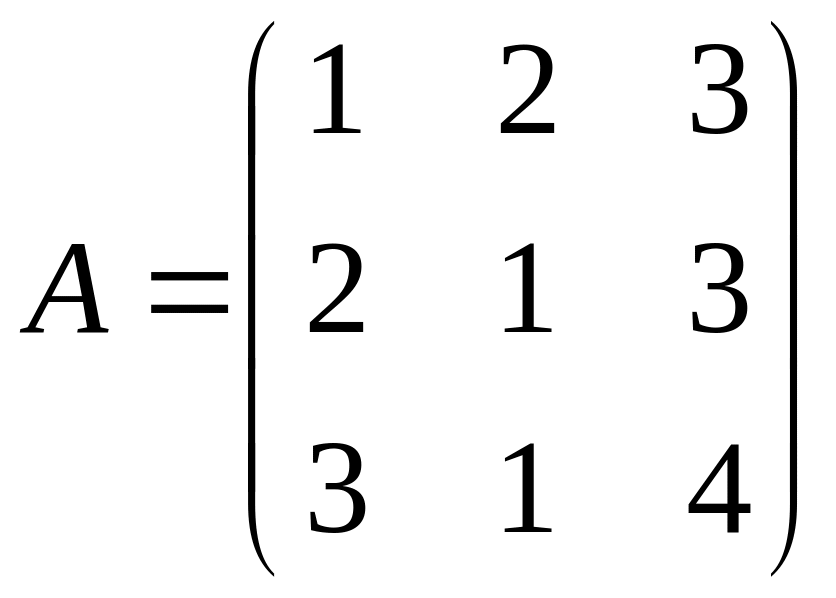Задание 4.
Вычислить ранг матрицы
.
Задание 5. Решить систему уравнений методом Гаусса-Жордано:
.
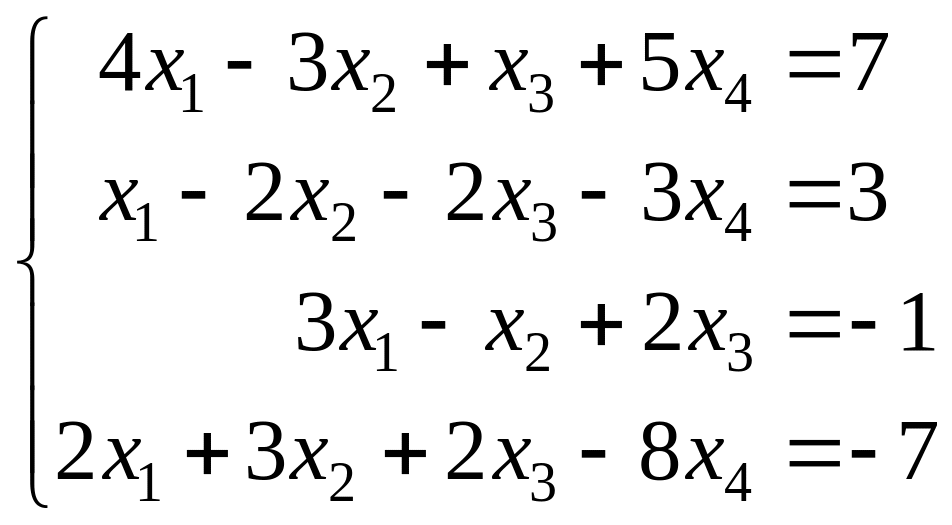Задание 6.
Найти общее и одно из частных решений
системы линейных уравнений:
.
Задание 7. Найти общее решение и фундаментальную систему решений:
.
Вариант 2.5
Задание 1.
Выполнить действия с матрицами:
.
Задание 2.
Вычислить определитель матрицы:
.
Задание 3.
Определить, имеет ли матрица
обратную, и, если имеет вычислить ее:
.
Задание 4.
Вычислить ранг матрицы
.
Задание 5. Решить систему уравнений методом Гаусса-Жордано:
.
Задание 6.
Найти общее и одно из частных решений
системы линейных уравнений:
.
Задание 7. Найти общее решение и фундаментальную систему решений:
.
Вариант 2.6
Задание 1.
Выполнить действия с матрицами:
.
Задание 2.
Вычислить определитель матрицы:
.
Задание 3.
Определить, имеет ли матрица
обратную, и, если имеет вычислить ее:
.
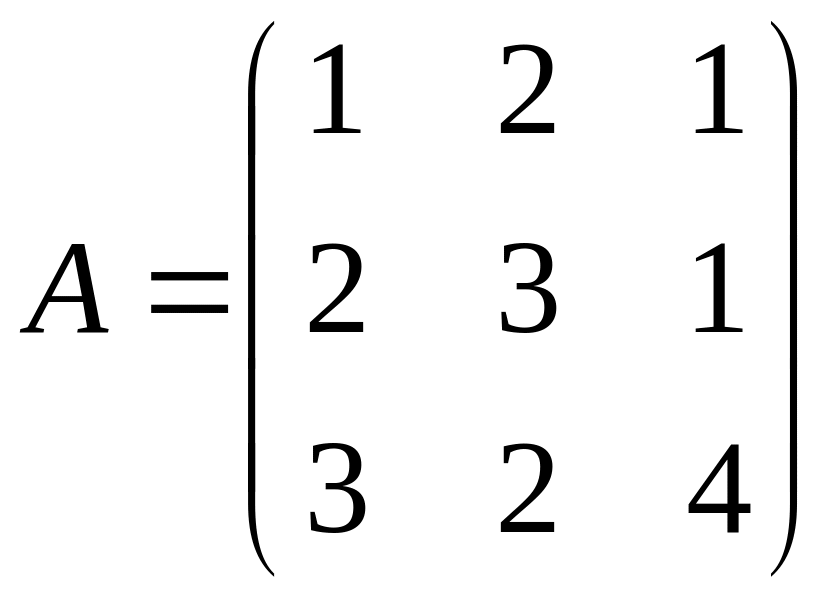Задание 4.
Вычислить ранг матрицы
.
Задание 5. Решить систему уравнений методом Гаусса-Жордано:
.
Задание 6.
Найти общее и одно из частных решений
системы линейных уравнений:
.
Задание 7. Найти общее решение и фундаментальную систему решений:
.
Вариант 2.7
Задание 1.
Выполнить действия с матрицами:
.
Задание 2.
Вычислить определитель матрицы:
.
Задание 3.
Определить, имеет ли матрица
обратную, и, если имеет вычислить ее:
.
Задание 4.
Вычислить ранг матрицы
.
Задание 5. Решить систему уравнений методом Гаусса-Жордано:
.
Задание 6. Найти общее и одно из частных решений системы линейных уравнений:
.
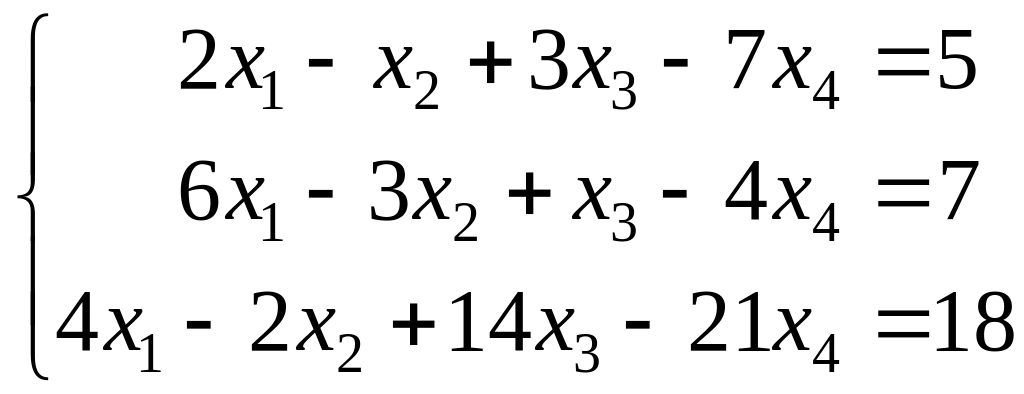Задание 7. Найти общее решение и фундаментальную систему решений:
.
Вариант 2.8
Задание 1.
Выполнить действия с матрицами:
.
Задание 2.
Вычислить определитель матрицы:
.
Задание 3.
Определить, имеет ли матрица
обратную, и, если имеет вычислить ее:
.
Задание 4.
Вычислить ранг матрицы
.
Задание 5. Решить систему уравнений матричным методом:
.
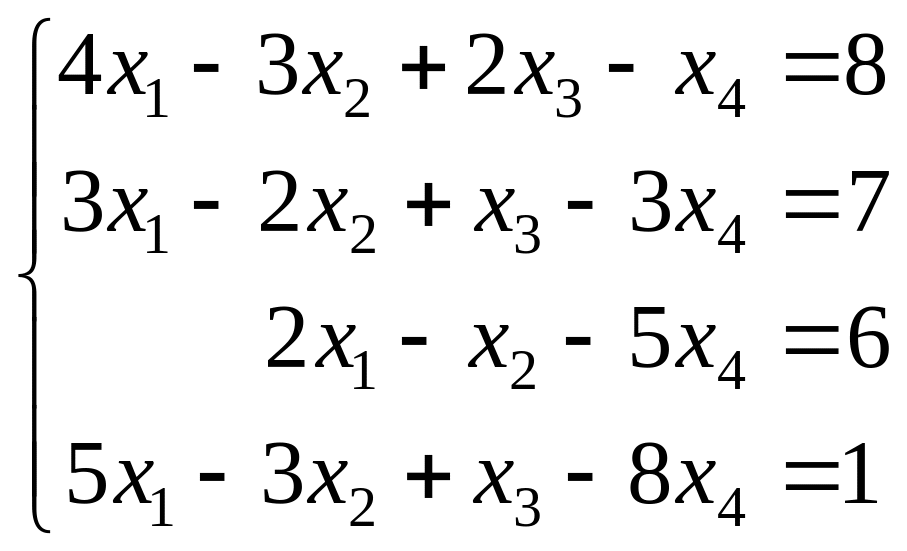Задание 6. Найти общее и одно из частных решений системы линейных уравнений:
.
Задание 7. Найти общее решение и фундаментальную систему решений:
.
Вариант 2.9
Задание 1.
Выполнить действия с матрицами:
.
Задание 2.
Вычислить определитель матрицы:
.
Задание 3.
Определить, имеет ли матрица
обратную, и, если имеет вычислить ее:
.
Задание 4.
Вычислить ранг матрицы
.
Задание 5. Решить систему уравнений матричным методом:
.
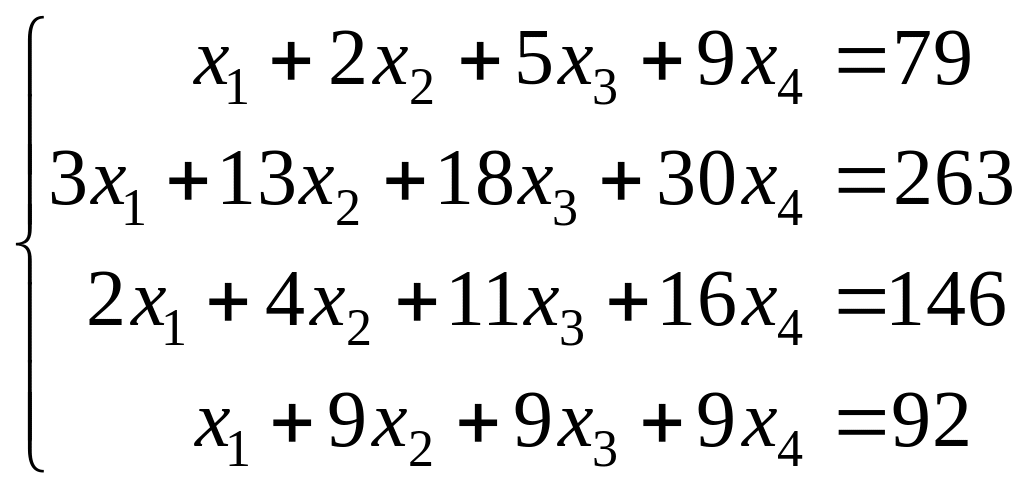Задание 6. Найти общее и одно из частных решений системы линейных уравнений:
.
Задание 7. Найти общее решение и фундаментальную систему решений:
.
Вариант 2.10
Задание 1.
Выполнить действия с матрицами:
.
Задание 2.
Вычислить определитель матрицы:
.
Задание 3.
Определить, имеет ли матрица
обратную, и, если имеет вычислить ее:
.
Задание 4.
Вычислить ранг матрицы
.
Задание 5. Решить систему уравнений матричным методом:
.
Задание 6. Найти общее и одно из частных решений системы линейных уравнений:
.
Задание 7. Найти общее решение и фундаментальную систему решений:
.
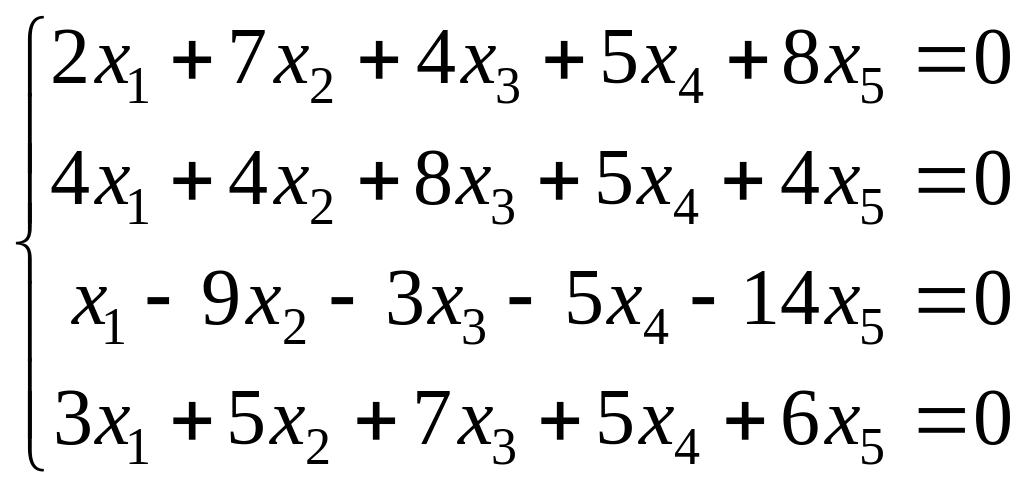