
- •Высшая математика I
- •Общие методические указания
- •Содержание
- •Основы векторной алгебры
- •Основные понятия векторной алгебры
- •Операции над векторами
- •Базис и разложение векторов
- •Скалярное произведение векторов
- •Определители 2-го и 3-го порядка
- •Векторное и смешанное произведения векторов
- •Примеры решения типовых задач: векторная алгебра
- •Аналитическая геометрия
- •Уравнение линии
- •Уравнение прямой на плоскости
- •Примеры решения типовых задач: прямая на плоскости
- •Уравнение плоскости
- •Примеры решения типовых задач: уравнение плоскости
- •Прямая в пространстве
- •Примеры решения типовых задач: прямая в пространстве
- •Кривые второго порядка
- •Примеры решения типовых задач: кривые второго порядка
- •Контрольная работа 1. Часть 1.
- •Пример выполнения контрольной работы 1 (часть 1)
- •Линейная алгебра
- •Матрицы
- •Примеры решения типовых задач: матрицы
- •Решение систем линейных уравнений
- •Примеры решения типовых задач: системы линейных уравнений
- •Контрольная работа 1. Часть 2.
- •Пример выполнения контрольной работы 1 (часть 2)
- •Введение в численные методы. Основные понятия
- •Интерполяция и квадратурные формулы
- •Контрольная работа 1. Часть 3.
- •Пример выполнения контрольной работы 1 (часть 3)1
- •Рекомендуемая основная литература
Примеры решения типовых задач: матрицы
Задача 4.1.
Вычислить матрицу
по правилу:
![]() ,
где
,
где
![]() ;
;
![]() ;
;
![]() .
.
Решение: По правилам выполнения арифметических операций, сначала выполняем операции, указанные в скобках. Найдем суммы матриц:
![]() ;
;
![]() .
.
Теперь найдем произведение полученных матриц:
![]() .
Ответ:
.
Ответ:
![]() .
.
Задача 4.2.
Вычислить матрицу
![]() ,
где
,
где
![]() ,
,
![]() .
.
Решение:
Вычислим вспомогательную матрицу
 :
:
![]()
Вычислим вспомогательную матрицу
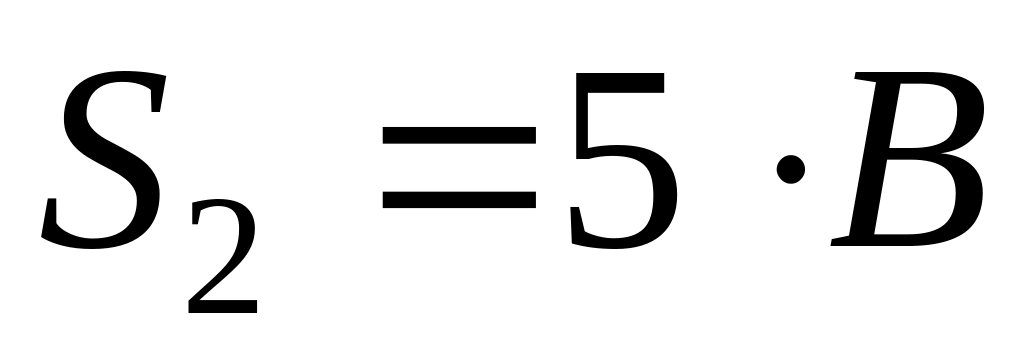 :
:
![]()
Вычислим матрицу
 .
.
![]()
![]() .
Ответ:
.
Ответ:
![]() .
.
Задача 4.3.
Вычислить
определитель матрицы:
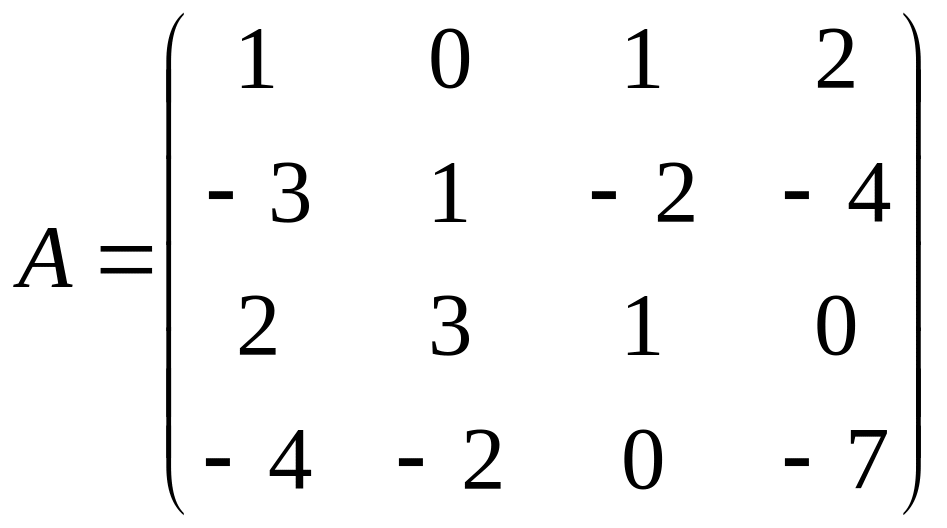 .
.
Решение. Преобразуем определитель так, чтобы в первой строке остались нули, кроме элемента в первом столбце. Один нуль уже есть, получим еще два. Для этого умножим элементы первого столбца на (-1) и сложим с элементами третьего столбца. Затем умножим элементы первого столбца на (-2) и сложим с четвертым столбцом. При этом, естественно, элементы первого столбца перепишем без изменения:
 {Раскладываем
определитель по элементам первой строки}
{Раскладываем
определитель по элементам первой строки}
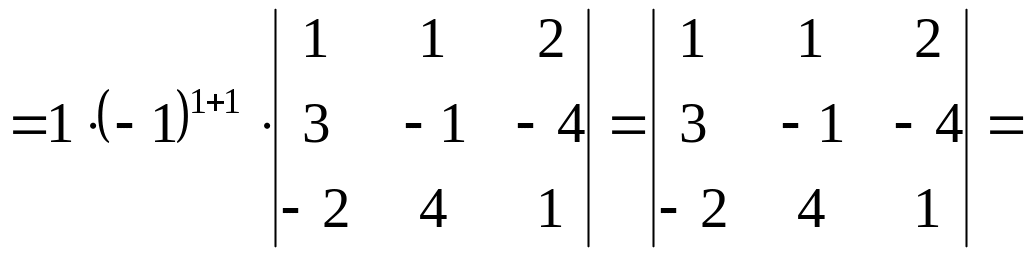 {Продолжим
преобразования определителя. Получим
в первой строке нули, кроме элемента в
первом столбце. Умножим элементы первого
столбца на (-1) и сложим с элементами
второго столбца. Затем умножим элементы
первого столбца на (-2) и сложим с элементами
третьего столбца. Разложим полученный
определитель по элементам первой строки}
{Продолжим
преобразования определителя. Получим
в первой строке нули, кроме элемента в
первом столбце. Умножим элементы первого
столбца на (-1) и сложим с элементами
второго столбца. Затем умножим элементы
первого столбца на (-2) и сложим с элементами
третьего столбца. Разложим полученный
определитель по элементам первой строки}
 .
Ответ:
.
Ответ:
![]() .
.
Задача
4.4.
Вычислить
обратную матрицу для
 .
.
Решение. 1) Вычислим определитель исходной матрицы, выполнив преобразования: умножим элементы первой строки на (-1) и сложим с элементами третьей строки. Затем разложим по элементам третьего столбца:
 .
.
2) Транспонируем
исходную матрицу
 .
.
3) Найдем алгебраические дополнения для каждого элемента полученной матрицы:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
4) Запишем алгебраические дополнения в транспонированную матрицу вместо ее элементов. Разделив каждый элемент матрицы на определитель исходной, получим обратную:
 .
.
Проверим выполнение условия :

 .
Ответ:
.
Ответ:
 .
.
Задача
4.5.
Вычислить матрицу, обратную к матрице:
 .
.
Решение. Вычислим определитель матрицы: сложим элементы третьего столбца с элементами первого и разложим по элементам третьего столбца:
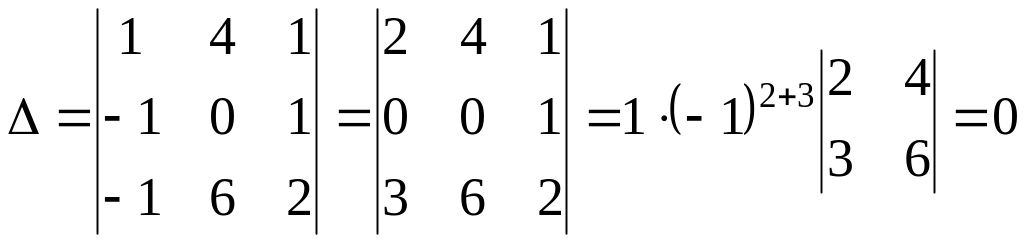 .
.
Определитель равен нулю, значит, матрица вырожденная и для нее обратной не существует.
Ответ: обратной матрицы не существует.
Задача
4.6.
Вычислить ранг матрицы:
 .
.
Решение. Матрица
имеет четыре столбца и три строки,
поэтому ее ранг не может превышать:
![]() .
Однако, она содержит нулевые столбцы:
второй и четвертый, значит все ее
подматрицы 3-го порядка также будут
содержать нулевые столбцы, и их
определитель будет равен нулю. Поэтому,
отбросив все нулевые столбцы имеем:
.
Однако, она содержит нулевые столбцы:
второй и четвертый, значит все ее
подматрицы 3-го порядка также будут
содержать нулевые столбцы, и их
определитель будет равен нулю. Поэтому,
отбросив все нулевые столбцы имеем:
 .
Полученная матрица имеет три строки и
два столбца, значит,
.
Полученная матрица имеет три строки и
два столбца, значит,
![]() .
Обратим внимание на элементы столбцов:
они пропорциональны, поэтому любые
подматрицы 2-го порядка, выделяемые из
данной, также будут иметь определители,
равные нулю. Следовательно, данная
матрица имеет ранг равный 1.
.
Обратим внимание на элементы столбцов:
они пропорциональны, поэтому любые
подматрицы 2-го порядка, выделяемые из
данной, также будут иметь определители,
равные нулю. Следовательно, данная
матрица имеет ранг равный 1.
Ответ:
![]() .
.
Задача 4.7.
Вычислить ранг матрицы:
 .
.
Решение. Поменяем местами первую и вторую строки, ранг матрицы от этого не изменится:

Преобразуем матрицу
так, чтобы все элементы первого столбца,
кроме
![]() были равны нулю. Умножим все элементы
первой строки на 2 и сложим с соответствующими
элементами третьей строки. Затем сложим
все элементы первой строки с соответствующими
элементами третьей строки:
были равны нулю. Умножим все элементы
первой строки на 2 и сложим с соответствующими
элементами третьей строки. Затем сложим
все элементы первой строки с соответствующими
элементами третьей строки:
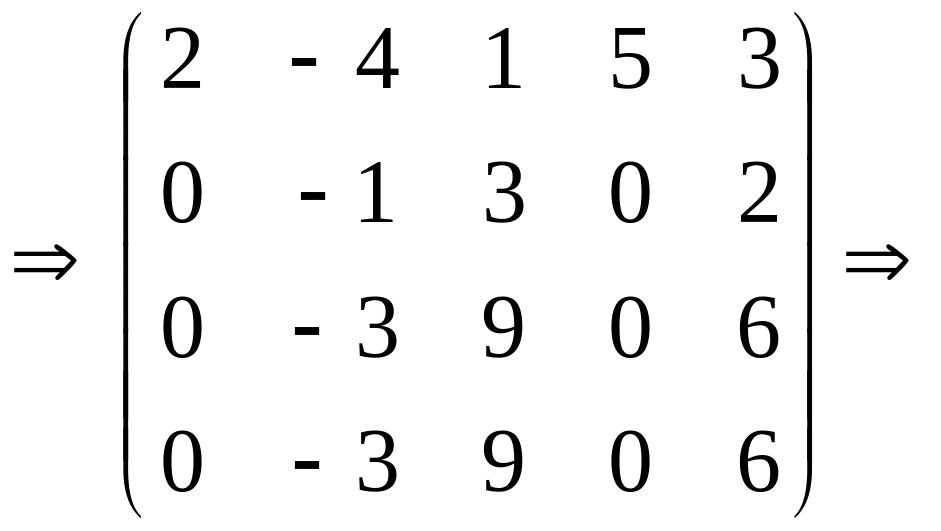 {Теперь
добиваемся, чтобы все элементы второго
столбца, кроме
{Теперь
добиваемся, чтобы все элементы второго
столбца, кроме
![]() и
и
![]() были равны нулю. Умножаем все элементы
второй строки на (-3) и складываем с
соответствующими элементами третьей
строки. Затем умножаем все элементы
второй строки на (-3) и складываем с
соответствующими элементами четвертой
строки. Если в процессе преобразований
получаются строки (или столбцы), целиком
состоящие из нулей, то отбрасываем их}
были равны нулю. Умножаем все элементы
второй строки на (-3) и складываем с
соответствующими элементами третьей
строки. Затем умножаем все элементы
второй строки на (-3) и складываем с
соответствующими элементами четвертой
строки. Если в процессе преобразований
получаются строки (или столбцы), целиком
состоящие из нулей, то отбрасываем их}
 .
.
Последняя матрица
содержит миноры второго порядка не
равные нулю, например:
![]() ,
следовательно,
,
следовательно,
![]() .
.
Ответ: .
