5. Збіжність в метричному просторі. Приклади.

О. Последовательность сходится к точке х, если любая окрестность точки х содержит все элементы последовательности, начиная с некоторого.

Точка х называется пределом последовательности.

Последовательность сходится к точке х, если предел расстояния равен нулю.

Теорема: Последовательность точек из R может сходится не более, чем к одному пределу.

Теорема: Для того, чтобы точка х была точкой прикосновения мн-ва М необходимо и достаточно, чтобы существовала последовательность точек из М, сходящихся к х.

Следствие: Для того, чтобы точка х была предельной точкой для множества М необх. и достаточно, чтобы в М существовала последовательность попарно различных точек, сходящихся к х.

6. Щільні, всюди щільні, ніде не щільні множини. Сепарабельні простори. Приклади.

Мн-во А называется плотным в В, если В .

Множество А называется всюду плотным, если оно плотно во всем пр-ве.

Мн-во А называется нигде не плотным, если оно не плотно ни в одном шаре.

Пространство, в котором существует счетное, всюду плотное мн-во называется сепарабельным.

Примеры: Дискретное пр-во является сепарабельным, если оно состоит из счетного числа элементов.

Пр.-во R является сепарабельным, если счетное всюду плотное множество в нем является мн-вом рациональных чисел.

Счетное, всюду плотным множеством в этих пространствах является множество векторов с рациональными координатами.

6. Является сепарабельным пр-вом, счетным всюду плотное мн-вом в этом пр-ве является мн-во всех многочленов с рациональными коэффициентами.

7.

8. сепарабельное, счетным всюду плотным мн-вом является множество многочленов с рациональными коэф-тами.

9. Пр-во m – единственное несепарабельное пр-во.

7. Повні метричні простори. Приклади , , .

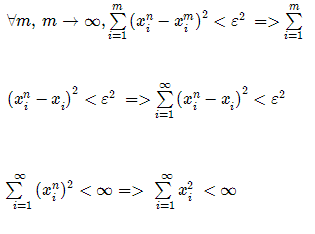
8. Теорема про вкладені кулі. Теорема Бєра

Теорема 2 (о вложенных шарах). Для того, чтобы метрическое пространство было полным необходимо и достаточно, чтобы в нём всякая последовательность вложенных друг в друга замкнутых шаров, радиусы которых стремятся к нулю, имела непустое пересечение.

Необходимость.

Рассмотрим полное метрическое пространство   и последовательность   вложенных друг в друга замкнутых шаров с центрами   и радиусами  : .

Последовательность центров   является фундаментальной, так как

,и .

Так как пространство   является полным, то последовательность   сходится и .

Шар   содержит все точки последовательность   кроме, быть может, точек  , а следовательно   — точка прикосновения любого из шаров  , так как шары предполагаются замкнутыми, отсюда следует, что .

По определению пересечения множеств .

Таким образом, пересечение шаров   действительно не является пустым множеством.

Достаточность.

Пусть   — фундаментальная последовательность, тогда можно указать такой номер  , что для   будет выполняться неравенство .

Обозначим .

Следующий номер   выберем таким образом, чтобы при   выполнялось неравенство .

Обозначим .

Пусть мы уже выбрали номера .

Номер   выберем так, чтобы при   выполнялось неравенство ,

Обозначим .

Продолжая этот процесс, мы получим последовательность замкнутых вложенных шаров, по предположению теоремы эта последовательность имеет общую точку, обозначим эту точку как  . Очевидно, что эта точка служит пределом последовательности  . Фундаментальная последовательность, содержащая сходящуюся подпоследовательность, сходится к тому же пределу, следовательно .

Так как последовательность взята произвольно, то метрическое пространство   является полным.

Теорема Бэрра. Полное метрическое пространство   не может быть представлено в виде объединения счётного числа нигде не плотных множеств.

Доказательство проведём от противного.

Пусть , причём каждое из множеств   нигде не плотно. Рассмотрим некоторый замкнутый шар   радиуса 1, так как множество   нигде не плотно, то оно не плотно и в шаре  , то есть существует шар  , радиус которого меньше  , такой, что .

Множество   не плотно в шаре  , значит существует шар  , радиус которого меньше  , для которого

,

и так далее. Таким образом можно получить последовательность вложенных друг в друга замкнутых шаров ,

радиусы которых стремятся к нулю, причём .

По теореме о вложенных шарах пересечение

содержит некоторую точку  , которая не принадлежит ни одному из  , так как ,

а значит точка   не принадлежит и объединению всех 

,то есть , что противоречит исходному предположению. Теорема доказана.