8. Конусність

Конусність (C або К) — відношення діаметра кола D основи конуса до його висоти H для повних кругових конусів або відношення різниці діаметрів D і d двох поперечних перерізів конуса до відстані h між ними для зрізаних конусів. Конусність зазвичай записується як відношення двох чисел, наприклад: 1:10; 1:12; 1:20.

  або  

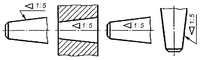  На технічних кресленнях значення конусності поверхонь деталей вказують у вигляді простого дробу або в процентах. Для машинобудівної промисловості стандарт установлює наступні значення конусності: 1:500; 1:200; 1:100; 1:50; 1:30; 1: 20; 1: I5; 1:12; 1: 10; 1: 8; 1:7; 1:5; 1:3; 30°; 45°; 60°; 75°; 90°; 120°

На кресленнях конусність позначають так. Перед розмірним числом, що характеризує конусність, наносять знак « », гострий кут якого має бути спрямований у бік вершини конуса.

Уклоном називають величину, що характеризує нахил прямої лінії від­носно іншої прямої (горизонтальної або вертикальної).

На малюнку а показано пряму СВ, яка має уклон відносно прямої АВ. Характеризують уклон відношенням довжин катетів прямокутного трикутника АВС:

О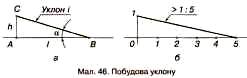 тже, якщо потрібно провести лінію з уклоном, наприклад 1 : 5 від­носно заданої (б), то до заданої прямої проводять перпендикуляр і на ньому відкладають один відрізок довільної довжини, а на заданій прямій - п'ять таких відрізків. Сполучивши між собою кінцеві точки обох відрізків, отримують заданий уклон.

У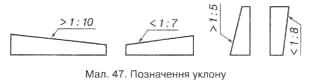 клони на кресленнях указують у вигляді числових співвідношень (1 : 3; 1 : 5; 1 : 8; 1:10; 1: 12 і т. д.) або у відсотках (10 %; 12 %). В цому випадку горизонтально відкладають 100% довжини (100мм), а вертикально – той самий процент (наприклад -12% - 12 мм.)

Перед числовим співвідношенням наносять знак <. Його гострий кут спрямову­ють у бік нахилу

9. Спряження. Три випадки спряження двох дуг за допомогою дуги заданого радіуса

С пряженням називають плавний перехід однієї лінії в іншу. Для побудови спряження потрібно знати центри спряження і точки спряження. Центри спряження – центр дуги спряження, а точки спряження – це точки в яких одна лінія переходить в іншу. 

Спряження двох даних кіл дугою заданого радіуса R₃.

З овнішнє спряження . Із центра О₁ кола радіуса R₁ описують дугу допоміжного кола радіусом, що дорівнює сумі радіусів R₁ + R₃. Із центра О₂ кола радіуса R₂ описують дугу допоміжного кола радіусом, що дорівнює сумі радіусів R₂ + R₃. Точка О₃ перетину цих двох дуг є центром спряження. Щоб знайти точки спряження А і В, з'єднують центр О₃ з центрами О₁ і О₂.

Внутрішнє спряження

З центра О₁ кола радіуса R₁ описують дугу допоміжного кола, радіус якого дорівнює різниці радіусів R₃-R₁, а з центра О₂ кола радіуса R₂ описуємо дугу, радіус якої дорівнює різниці радіусів R₃ –R₂.

Точка перетину цих дуг є центром спряження О₃. Щоб знайти точки спряження А і В, з'єднують центр О₃ з центрами О₁ і О₂.

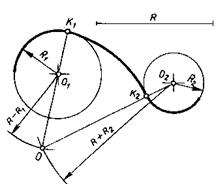
Змішане спряження

Із центра О₁ проводять дугу радіусом, що дорівнює R-R₁, а із центра О₂ - радіусом R+R₂. Перетин проведених дуг визначає центр дуги спряження. Дуга спряження має з дугою радіуса R₁ внутрішнє спряження, а з дугою радіуса R₂ - зовнішнє. Точка K₁ є точкою самодотикання, а точка К₂ - точкою перегину