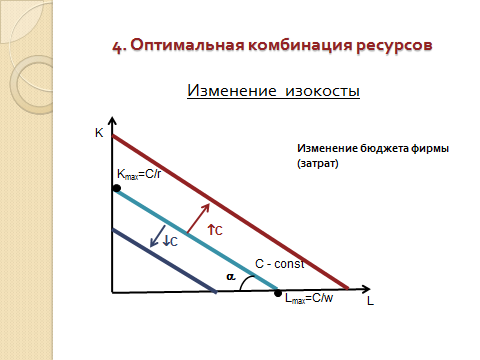
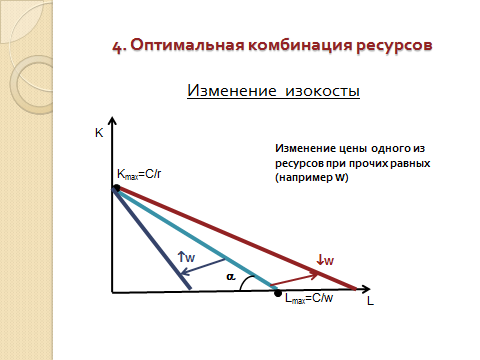
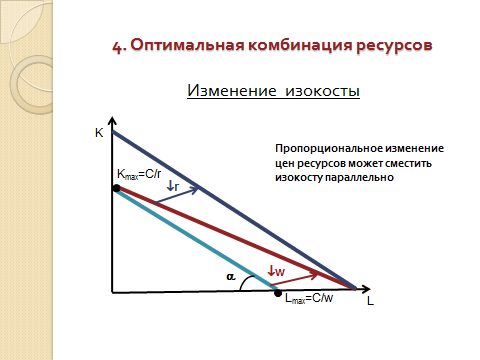
10. Что представляет собой изокоста? От чего зависит наклон изокосты?

Роль бюджетной прямой в теории производства выполняет линия равных затрат – изокоста, представляющая множество всех комбинаций ресурсов, которые могли бы быть приобретены предприятием при определенной сумме денежных расходов:

K=C/r – w/r*L

Наклон линии изокосты определяется отношением рыночных цен на труд и на капитал что вытекает из уравнения изокосты.

В точке касания изокванты и изокосты наклоны их совпадают( точка оптимума):

-наклон изокосты равен w/r

-наклон изокванты равен MRTS_LK

В точке оптимума производителя выполняется равенство: MRTS_LK= w/r

Подробнее: MRTS_LK= MP_L/MP_K=w/r

11. Что представляет собой оптимальная линия роста?

В длительном периоде расширение производства идет в соответствии с «оптимальным путем развития» ( оптимальным путем роста)- ОР.

Если производственная функция однородна, оптимальный путь роста-это луч, выходящий из начала координат, наклон которого определяет оптимальное соотношение K/L и зависит от соотношения цен ресурсов.

12. Что представляет собой функция Кобба-Дугласа?

Наиболее простой является двухфакторная модель производственной функции Кобба – Дугласа, с помощью которой раскрывается взаимосвязь труда (L) и капитала (К). Типичной Q=AL^αK^β, 0<α<1, 0<β<1, где А,α,β – положительные постоянные числа, характеризующие технологию производства.

Показатели α и βстепенной производственной функции равны коэффициентам эластичности выпуска по факторам:

Ɛ_Q,L= MP_L/AP_L= αAK^βL^α-1/ AK^βL^α-1= α

Ɛ_Q,K= MP_K/AP_K= βAL^αK^β-1/ AL^αK^β-1= β

На основе анализа коэффициентов эластичности в производственной функции Кобба - Дугласа можно выделить:

1. пропорционально возрастающую производственную функцию, когда  α+ β=1

2. непропорционально – возрастающую α+ β>1

3. убывающую α+ β<1