
- •Последовательность .
- •Теорема о представлении сходящейся числовой последовательности.
- •Предел частного двух сходящихся числовых последовательностей.
- •Предельный переход в неравенствах.
- •Теорема о сжатой последовательности.
- •Критерий сходимости монотонной числовой последовательности.
- •Теоремы о вложенных и стягивающихся отрезках.
- •Принцип выбора (теорема Больцано-Вейерштрасса).
- •Критерий Гейне существования предела функции.
- •Стабилизация знака непрерывной функции.
- •Непрерывность сложной функции.
- •Теорема о непрерывности монотонной функции.
- •Теорема о непрерывности обратной функции.
- •Непрерывность тригонометрических функций.
- •Теорема о представлении эквивалентных функций.
- •Теорема Больцано-Коши (о промежуточном значении функции).
- •Первая теорема Вейерштрасса (об ограниченности функции на отрезке).
- •Вторая теорема Вейерштрасса (о достижимости точных границ).
- •Теорема Кантора (о равномерной непрерывности функции).
- •Дифференцирование произведения двух функций.
- •Дифференцирование обратной функции.
- •Теоремы Ферма, Ролля, Коши и Лагранжа для дифференцируемых функций
- •Тэарэма Кашы. Калі функцыі і – непарыўныя на , дыферэнцавальныя на і , то
- •Тэарэма Лягранжа. Калі функцыя ёсць непарыўная на , і дыферэнцавальныя на , то . (2)
- •Рекуррентная формула вычисления .
- •Интегрирование биномного дифференциала (подстановки Чебышёва).
- •Интегрируемость функции, непарывнойй на отрезке. Тэарэма 1 (Інтэгравальнасць непарыўнай функцыі). Непарыўная на адрэзку функцыя ёсць інтэгравальная на гэтым адрэзку.
- •Вынік 2 (Тэарэма пра пасярэдняе значэнне непарыўнай функцыі). Калі функцыя ёсць непарыўная, то існуе лік такі, што
- •Дифференцируемость интеграла с переменной верхней границей (теорема Барроу).
- •Калі функцыя ёсць непарыўная на , то функцыя ёсць дыферэнцавальная на , прычым .
Интегрируемость функции, непарывнойй на отрезке. Тэарэма 1 (Інтэгравальнасць непарыўнай функцыі). Непарыўная на адрэзку функцыя ёсць інтэгравальная на гэтым адрэзку.
□ Няхай
функцыя
![]() ёсць непарыўная на адрэзку
ёсць непарыўная на адрэзку
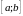 .
Паводле тэарэмы Кантара яна раўнамерна
непарыўная на гэтым адрэзку, г.зн. мае
месца (1).
.
Паводле тэарэмы Кантара яна раўнамерна
непарыўная на гэтым адрэзку, г.зн. мае
месца (1).
Няхай
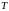 – такі падзел адрэзка
,
што яго дробнасць
– такі падзел адрэзка
,
што яго дробнасць
 .
Адпаведна другой тэарэме Ваерштраса
.
Адпаведна другой тэарэме Ваерштраса
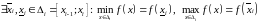 .
.
Паколькі
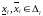 ,
а
,
то
,
а
,
то
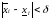
 ,
а таму
,
а таму
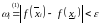 .
Маем
.
Маем
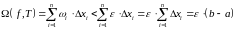 ,г.зн.
,г.зн.
 .
.
Згодна з крытэрам інтэгравальнасці функцыя ёсць інтэгравальная на . ■
Можна даказаць праўдзівасць наступных тэарэм:
Тэарэма 2 (Інтэгравальнасць кавалкава-непарыўнай функцыі). Калі функцыя , вызначаная і абмежаваная на адрэзку, ёсць непарыўная ва ўсіх пунктах гэтага адрэзку акрамя іх канечнай колькасці (г.зн ёсць кавалкава-непарыўная), то яна інтэгравальная на гэтым адрэзку.
Тэарэма 3 (Інтэгравальнасць манатоннай функцыі). Калі функцыя вызначана, абмежаваная і манатонная на адрэзку, то яна інтэгравальная на гэтым адрэзку.
Тэарэма 4
(Інтэгравальнасць
кампазіцыі). Калі
функцыя
інтэгравальная на адрэзку
і
 ,
а функцыя
,
а функцыя
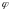 непарыўная на
непарыўная на
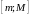 ,
то складаная функцыя
,
то складаная функцыя
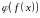 ёсць інтэгравальная на
.
ёсць інтэгравальная на
.
Теоремы о среднем значении интегрируемой и непрерывной функций.
Тэарэма (Абагульненая тэарэма пра пасярэдняе значэнне інтэгравальнай функцыі). Калі функцыі і ёсць інтэгравальныя на адрэзку , а функцыя не змяняе знаку на , то існуе лік
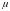 ,
,
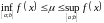 такі, што
такі, што
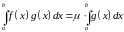 (1).
(1).
□ Няхай
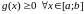 .
Паколькі
інтэгравальная на
,
то яна абмежаваная на
,
а г. зн.
.
Паколькі
інтэгравальная на
,
то яна абмежаваная на
,
а г. зн.
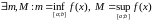 .
Пры гэтым маем
.
Пры гэтым маем
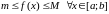 .
Адсюль, паколькі
.
Адсюль, паколькі
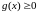 ,
маем
,
маем
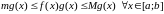
Паколькі
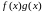 ёсць інтэгравальная на
ёсць інтэгравальная на
![]() , то згодна з уласцівасцю манатоннасці
інтэграла маем
, то згодна з уласцівасцю манатоннасці
інтэграла маем
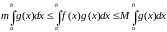 .
(2)
.
(2)
Калі
пры гэтым
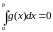 ,
то
,
то
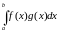 таксама роўны нулю і роўнасць (1)
праўдзіцца пры кожным
.
таксама роўны нулю і роўнасць (1)
праўдзіцца пры кожным
.
Калі ж
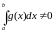 , то
, то
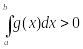 ,
і няроўнасць (2) можна падзяліць на гэты
,
і няроўнасць (2) можна падзяліць на гэты
інтэграл.
Атрымаем
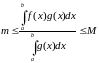 .
Абазначым
.
Абазначым
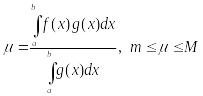 .
З гэтай роўнасці і атрымліваецца (1).
.
З гэтай роўнасці і атрымліваецца (1).
Калі ж
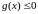 ,
то для функцыі
,
то для функцыі
![]() мае месца (1), г. зн.
мае месца (1), г. зн.
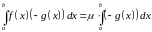 .
.
Дамнажаючы абедзве часткі гэтай роўнасці на –1, атрымаем (1). ■
Вынік 1. (Тэарэма пра пасярэдняе значэнне інтэгравальнай функцыі). Калі функцыя ёсць інтэгравальная на адрэзку , то існуе лік , такі, што
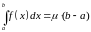 .
(2)
.
(2)
□ Калі
ў тэарэме 1 узяць
![]() ,
то атрымаем
,
то атрымаем
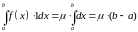 ■
■
Заўвага.
Лік
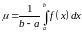 называецца сярэднім значэннем функцыі
на
.
называецца сярэднім значэннем функцыі
на
.
Вынік 2 (Тэарэма пра пасярэдняе значэнне непарыўнай функцыі). Калі функцыя ёсць непарыўная, то існуе лік такі, што
□ Для
функцыі f
згодна з вынікам 1 мае месца формула
(2),
дзе
.
Паколькі f
непарыўная на
,
то, на падставе другой тэарэмы Ваерштраса
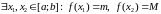 ,
дзе
,
дзе
![]() .
Паколькі
.
Паколькі
![]() ,
то згодна з тэарэмаю Бальцана-Кашы аб
прамежкавым значэнні непарыўнай функцыі
,
то згодна з тэарэмаю Бальцана-Кашы аб
прамежкавым значэнні непарыўнай функцыі
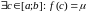 .
Падстаўляючы ў (1) замест
.
Падстаўляючы ў (1) замест
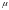 значэнне
значэнне
![]() ,
атрымаем (3). ■
,
атрымаем (3). ■
Заўвага.
Мы даказалі, што калі
непарыўная на адрэзку
,
то
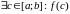 – сярэдняе значэне функцыі
на адрэзку
.
– сярэдняе значэне функцыі
на адрэзку
.
Дифференцируемость интеграла с переменной верхней границей (теорема Барроу).
Тэарэма Барроў (Дыферэнцавальнасць інтэграла са зменнаю верхняю мяжою).
