
- •Последовательность .
- •Теорема о представлении сходящейся числовой последовательности.
- •Предел частного двух сходящихся числовых последовательностей.
- •Предельный переход в неравенствах.
- •Теорема о сжатой последовательности.
- •Критерий сходимости монотонной числовой последовательности.
- •Теоремы о вложенных и стягивающихся отрезках.
- •Принцип выбора (теорема Больцано-Вейерштрасса).
- •Критерий Гейне существования предела функции.
- •Стабилизация знака непрерывной функции.
- •Непрерывность сложной функции.
- •Теорема о непрерывности монотонной функции.
- •Теорема о непрерывности обратной функции.
- •Непрерывность тригонометрических функций.
- •Теорема о представлении эквивалентных функций.
- •Теорема Больцано-Коши (о промежуточном значении функции).
- •Первая теорема Вейерштрасса (об ограниченности функции на отрезке).
- •Вторая теорема Вейерштрасса (о достижимости точных границ).
- •Теорема Кантора (о равномерной непрерывности функции).
- •Дифференцирование произведения двух функций.
- •Дифференцирование обратной функции.
- •Теоремы Ферма, Ролля, Коши и Лагранжа для дифференцируемых функций
- •Тэарэма Кашы. Калі функцыі і – непарыўныя на , дыферэнцавальныя на і , то
- •Тэарэма Лягранжа. Калі функцыя ёсць непарыўная на , і дыферэнцавальныя на , то . (2)
- •Рекуррентная формула вычисления .
- •Интегрирование биномного дифференциала (подстановки Чебышёва).
- •Интегрируемость функции, непарывнойй на отрезке. Тэарэма 1 (Інтэгравальнасць непарыўнай функцыі). Непарыўная на адрэзку функцыя ёсць інтэгравальная на гэтым адрэзку.
- •Вынік 2 (Тэарэма пра пасярэдняе значэнне непарыўнай функцыі). Калі функцыя ёсць непарыўная, то існуе лік такі, што
- •Дифференцируемость интеграла с переменной верхней границей (теорема Барроу).
- •Калі функцыя ёсць непарыўная на , то функцыя ёсць дыферэнцавальная на , прычым .
Первая теорема Вейерштрасса (об ограниченности функции на отрезке).
Першая
тэарэма Ваерштраса (пра
абмежаванасць функцыі). Калі
функцыя f
ёсць непарыўная на адрэзку
,
то яна абмежаваная на гэтым адрэзку,
г.зн.
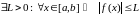 .
.
□ (ад процілеглага) Няхай f – неабмежаваная на , г. зн.
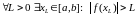 .
.
Возьмем
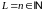 і тым самым пабудуем лікавую паслядоўнасць
і тым самым пабудуем лікавую паслядоўнасць
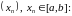
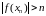 ,
,
г. зн.
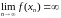 .
Паколькі
–
абмежаваная
.
Паколькі
–
абмежаваная
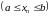 ,
то згодна з тэарэмаю Бальцана-Ваерштраса
(прынцып выбару) з яе можна вылучыць
збежную падпаслядоўнасць
,
то згодна з тэарэмаю Бальцана-Ваерштраса
(прынцып выбару) з яе можна вылучыць
збежную падпаслядоўнасць
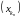 .
Няхай
–яе
ліміт. Паколькі
.
Няхай
–яе
ліміт. Паколькі
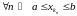 ,
то з тэарэмы пра лімітавы пераход у
няроўнасці маем
,
то з тэарэмы пра лімітавы пераход у
няроўнасці маем
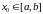 .
Паколькі f
–непарыўная у пункце
,
то
.
Паколькі f
–непарыўная у пункце
,
то
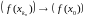 ,
але гэта немагчыма, паколькі
,
але гэта немагчыма, паколькі
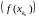 –бясконца
вялікая паслядоўнасць як падпаслядоўнасць
бясконца вялікай паслядоўнасці
–бясконца
вялікая паслядоўнасць як падпаслядоўнасць
бясконца вялікай паслядоўнасці
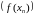 .
Такім чынам, дапушчэнне непраўдзівае,
а тым самым f
– абмежаваная. ■
.
Такім чынам, дапушчэнне непраўдзівае,
а тым самым f
– абмежаваная. ■
Вторая теорема Вейерштрасса (о достижимости точных границ).
Другая тэарэма Ваерштраса (пра дасягальнасць дакладных межаў). Калі функцыя f непарыўная на адрэзку , то яна дасягае на гэтым адрэзку сваіх дакладных ніжняй і верхняй межаў, г. зн.
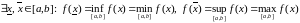 .
.
□ Згодна
з першаю тэарэмаю Ваерштраса функцыя
f–
абмежаваная
на
,
а таму, на падставе тэарэмы пра межы,
існуюць
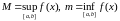 .
Пакажам, што існуе
.
Пакажам, што існуе
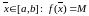 .
.
Дапусцім
процілеглае, г. зн.
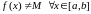 .
Паколькі
.
Паколькі
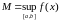 ,
то
,
то
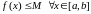 ,
а паколькі
,
а паколькі
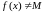 ,
то
,
то
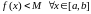 .
Таму функцыя
.
Таму функцыя
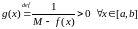 і непарыўная на
.
Згодна з першаю тэарэмаю Ваерштраса
функцыя g
–
абмежаваная
на
,
г. зн.
і непарыўная на
.
Згодна з першаю тэарэмаю Ваерштраса
функцыя g
–
абмежаваная
на
,
г. зн.
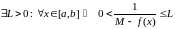 .
Адкуль маем
.
Адкуль маем
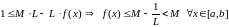 ,
а гэта азначае , што
,
а гэта азначае , што
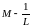 ёсць верхняя мяжа, а таму M
– не найменшая з верхніх межаў ?!? Такім
чынам,
ёсць верхняя мяжа, а таму M
– не найменшая з верхніх межаў ?!? Такім
чынам,
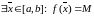 .
.
Аналагічна даказваецца другая частка тэарэмы. ■
Теорема Кантора (о равномерной непрерывности функции).
Тэарэма Кантара. Калі функцыя ёсць непарыўная на адрэзку, то яна раўнамерна непарыўная на гэтым адрэзку.
□ (ад процілеглага) Няхай функцыя f(x) ёсць непарыўная на адрэзку [a,b], але не з’яўляецца раўнамерна непарыўнаю на гэтым адрэзку:
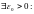
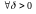
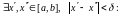
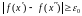 .
.
Возьмем
адвольную паслядоўнасць:
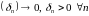 .
Для кожнага такога
.
Для кожнага такога
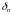 знойдуцца
знойдуцца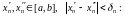
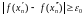 .
(1)
.
(1)
Паколькі
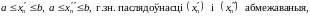 то згодна з прынцыпам выбару з паслядоўнасці
то згодна з прынцыпам выбару з паслядоўнасці
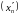 можна вылучыць збежную падпаслядоўнасць
можна вылучыць збежную падпаслядоўнасць
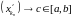 .
Калі з паслядоўнасці
.
Калі з паслядоўнасці
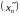 вылучыць падпаслядоўнасць
вылучыць падпаслядоўнасць
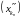 з адпаведнымі нумарамі
з адпаведнымі нумарамі
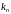 ,
то атрыманая падпаслядоўнасць таксама
збягаецца да ліміту c,
,
то атрыманая падпаслядоўнасць таксама
збягаецца да ліміту c,
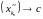 ,
што вынікае з няроўнасцяў
,
што вынікае з няроўнасцяў
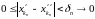 .
Функцыя f
непарыўная на [a,b]
і
,
таму
.
Функцыя f
непарыўная на [a,b]
і
,
таму
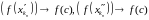 .
Але з (1) вынікае, што
.
Але з (1) вынікае, што
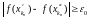 ,
адкуль, пераходзячы да ліміту, маем
,
адкуль, пераходзячы да ліміту, маем
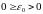 ?!? ■
?!? ■
Дифференцирование произведения двух функций.
Тэарэма .
Калі функцыі u
і v
ёсць дыферэнцавальныя ў пункце x,
то ў гэтым пункце дыферэнцавальныя
сума, розніца, здабытак і дзель гэтых
функцый. Пры гэтым праўдзяцца формулы:
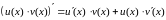 □
□
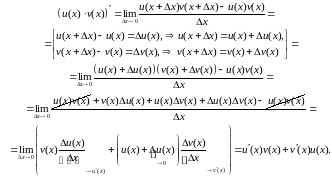
Далей
атрымаем формулу для вылічэння вытворнай
функцыі
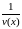 .
.
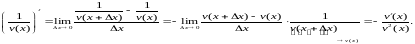 Калі
функцыю
Калі
функцыю
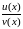 падаць у выглядзе
падаць у выглядзе
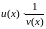 і выкарыстаць даказаныя дзве формулы,
то атрымаецца формула вылічэння вытворнай
дзелі. ■
і выкарыстаць даказаныя дзве формулы,
то атрымаецца формула вылічэння вытворнай
дзелі. ■
Дифференцирование обратной функции.
Тэарэма.
Калі строга манатонная і непарыўная на
прамежку Х функцыя
ёсць дыферэнцавальная ў пункце
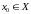 і
і
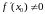 ,
то адваротная функцыя
,
то адваротная функцыя
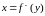 ёсць таксама дыферанцавальная ў
адпаведным пункце
ёсць таксама дыферанцавальная ў
адпаведным пункце
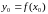 і яе вытворная ёсць
і яе вытворная ёсць
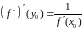 .
.
□ На
падставе тэарэмы пра адваротную функцыю,
функцыя
ёсць непарыўная на прамежку
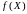 .
Таму пры
.
Таму пры
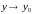 мае месца
мае месца
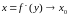 .
Маем
.
Маем
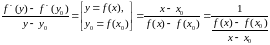 .
Пры пераходзе да ліміту пры
(пры гэтым
.
Пры пераходзе да ліміту пры
(пры гэтым
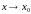 )
маем
.■
)
маем
.■
