
- •Последовательность .
- •Теорема о представлении сходящейся числовой последовательности.
- •Предел частного двух сходящихся числовых последовательностей.
- •Предельный переход в неравенствах.
- •Теорема о сжатой последовательности.
- •Критерий сходимости монотонной числовой последовательности.
- •Теоремы о вложенных и стягивающихся отрезках.
- •Принцип выбора (теорема Больцано-Вейерштрасса).
- •Критерий Гейне существования предела функции.
- •Стабилизация знака непрерывной функции.
- •Непрерывность сложной функции.
- •Теорема о непрерывности монотонной функции.
- •Теорема о непрерывности обратной функции.
- •Непрерывность тригонометрических функций.
- •Теорема о представлении эквивалентных функций.
- •Теорема Больцано-Коши (о промежуточном значении функции).
- •Первая теорема Вейерштрасса (об ограниченности функции на отрезке).
- •Вторая теорема Вейерштрасса (о достижимости точных границ).
- •Теорема Кантора (о равномерной непрерывности функции).
- •Дифференцирование произведения двух функций.
- •Дифференцирование обратной функции.
- •Теоремы Ферма, Ролля, Коши и Лагранжа для дифференцируемых функций
- •Тэарэма Кашы. Калі функцыі і – непарыўныя на , дыферэнцавальныя на і , то
- •Тэарэма Лягранжа. Калі функцыя ёсць непарыўная на , і дыферэнцавальныя на , то . (2)
- •Рекуррентная формула вычисления .
- •Интегрирование биномного дифференциала (подстановки Чебышёва).
- •Интегрируемость функции, непарывнойй на отрезке. Тэарэма 1 (Інтэгравальнасць непарыўнай функцыі). Непарыўная на адрэзку функцыя ёсць інтэгравальная на гэтым адрэзку.
- •Вынік 2 (Тэарэма пра пасярэдняе значэнне непарыўнай функцыі). Калі функцыя ёсць непарыўная, то існуе лік такі, што
- •Дифференцируемость интеграла с переменной верхней границей (теорема Барроу).
- •Калі функцыя ёсць непарыўная на , то функцыя ёсць дыферэнцавальная на , прычым .
Критерий Гейне существования предела функции.
Тэарэма.
(крытэр
Гайне існавання ліміту функцыі). Для
таго каб функцыя
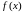 мела лімітам лік
мела лімітам лік
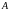 у пункце
у пункце
 ,
неабходна і дастаткова, каб для кожнай
лікавай паслядоўнасці
значэнняў аргумента функцыі
,
,
неабходна і дастаткова, каб для кожнай
лікавай паслядоўнасці
значэнняў аргумента функцыі
,
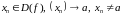 адпаведная лікавая паслядоўнасць
значэнняў функцыі
адпаведная лікавая паслядоўнасць
значэнняў функцыі
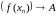 .
.
□ Неабходнасць.
Няхай
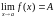 ,
г.зн.
,
г.зн.
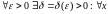 ,
,
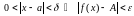 .
Возьмем адвольную лікавую паслядоўнасць
.
Возьмем адвольную лікавую паслядоўнасць
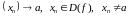 .
Яе
збежнасць азначае, што калі ўзяць выбраны
лік
.
Яе
збежнасць азначае, што калі ўзяць выбраны
лік
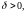 то
то
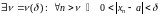 ,
а для такіх
,
а для такіх
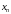 выконваецца няроўнась
выконваецца няроўнась
 .
Гэта і азначае, што
.
.
Гэта і азначае, што
.
Дастатковасць.
Няхай для кожнай лікавай паслядоўнасці
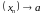 мае месца
мае месца
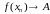 .
Дакажам, што
.
.
Дакажам, што
.
(ад
процілеглага)
Дапусцім, што
не ёсць ліміт функцыі
пры
.
Гэта азначае:
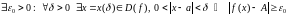 .
Возьмем адвольную лікавую паслядоўнасць
.
Возьмем адвольную лікавую паслядоўнасць
 .
Пасля гэтага
.
Пасля гэтага
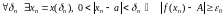 .
Мы пабудавалі лікавую паслядоўнасць
.
Мы пабудавалі лікавую паслядоўнасць
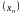 ,
якая мае ліміт
,
якая мае ліміт
 .
Чаму? (Паколькі
.
Чаму? (Паколькі
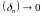 .)
Але пры гэтым
.)
Але пры гэтым
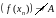 .
?!? ■
.
?!? ■
Стабилизация знака непрерывной функции.
Тэарэма.
Калі
функцыя
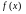 вызначана ў акрузе пункта
вызначана ў акрузе пункта
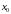 ,
непарыўная ў пункце
і
,
непарыўная ў пункце
і
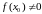 ,
то існуе акруга пункта
,
у якой знак функцыі
супа-дае з яе знакам у пункце
,
г.зн.
,
то існуе акруга пункта
,
у якой знак функцыі
супа-дае з яе знакам у пункце
,
г.зн.
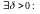
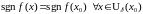 .
.
□
Няхай
для пэўнасці
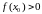 .
З прычыны непарыўнасці
у пункце
для
.
З прычыны непарыўнасці
у пункце
для
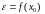

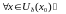
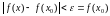

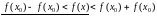 ,
адкуль вынікае, што
,
адкуль вынікае, што
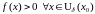 .
Выпадак
.
Выпадак
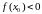 разглядаецца аналагічна (выбіраецца
разглядаецца аналагічна (выбіраецца
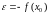 )
■
)
■
Непрерывность сложной функции.
def:
Няхай функцыя
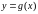 вызначана
на
вызначана
на
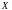 ,
а функцыя
,
а функцыя
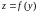 вызначана на
вызначана на
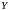 ,
прычым
,
прычым
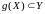 .
Тады функцыю, якая
.
Тады функцыю, якая
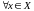 набывае значэнне
набывае значэнне
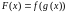 ,
называюць складанай
функцыяй
(або
кампазіцыяй,
або суперпазіцыяй)
функцый
,
называюць складанай
функцыяй
(або
кампазіцыяй,
або суперпазіцыяй)
функцый
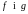 і абазначаюць
і абазначаюць
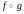 .
.
Тэарэма.
Калі
функцыя
непарыўная ў пункце
,
прычым
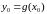 ,
а функцыя
непарыўная ў пункце
,
а функцыя
непарыўная ў пункце
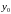 ,
то складаная функцыя
,
то складаная функцыя
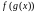 непарыўная ў пункце
.
непарыўная ў пункце
.
□ Паколькі
функцыя
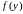 ёсць непарыўная ў пункце
,
то
ёсць непарыўная ў пункце
,
то
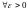
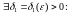
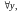
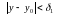 (1)
мае месца
(1)
мае месца
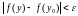 .
(2)
.
(2)
З
непарыўнасці функцыі
ў пункце
маем: для знойдзенага
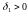 існуе
існуе
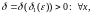
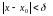 (3) выконваецца няроўнасць
(3) выконваецца няроўнасць
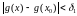 (4).
(4).
Калі ў
(4) і (2) узяць
і
,
то з (3) і (2) на падставе (1), (4) маем:
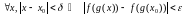 .
Гэта і азначае, што
– непарыўная ў пункце
.
■
.
Гэта і азначае, што
– непарыўная ў пункце
.
■
Теорема о непрерывности монотонной функции.
def:
Функцыю
называюць нарастальнай
на
мностве
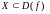 ,
калі
,
калі
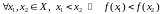 ;
неспадальнай,
калі
;
неспадальнай,
калі
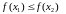 ;
спадальнай,
калі
;
спадальнай,
калі
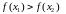 ;
ненарастальнай,
калі
;
ненарастальнай,
калі
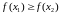 .
Усе такія функцыі называюцца манатоннымі.
Нарастальныя і спадальныя функцыі
называюцца строга
манатоннымі.
.
Усе такія функцыі называюцца манатоннымі.
Нарастальныя і спадальныя функцыі
называюцца строга
манатоннымі.
Тэарэма (пра
непарыўнасць манатоннай функцыі). Калі
функцыя
ёсць манатонная на адрэзку
 і мноства яе значэнняў ёсць адрэзак, то
яна непарыўная на адрэзку
.
і мноства яе значэнняў ёсць адрэзак, то
яна непарыўная на адрэзку
.
□ (ад
процілеглага)
Няхай
ёсць разрыўная на
і няхай
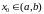 – яе пункт разрыву (для большай зручнасці
разглядаем выпадак пункта разрыву
ўнутры адрэзка). Для пэўнасці няхай
ёсць неспадальная. Тады згодна з
тэарэмай 1 або
– яе пункт разрыву (для большай зручнасці
разглядаем выпадак пункта разрыву
ўнутры адрэзка). Для пэўнасці няхай
ёсць неспадальная. Тады згодна з
тэарэмай 1 або
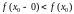 ,
або
,
або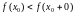 .
Няхай
.
Паколькі
неспадальная, то
.
Няхай
.
Паколькі
неспадальная, то
 (лімітавы
пераход ў няроўнасці), а для
(лімітавы
пераход ў няроўнасці), а для
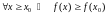 .
Гэта азначае, што
не набывае значэнняў з інтэрвала
.
Гэта азначае, што
не набывае значэнняў з інтэрвала
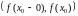 , г.зн. мноства значэнняў функцыі
не ёсць адрэзак.
, г.зн. мноства значэнняў функцыі
не ёсць адрэзак.
Аналагічна,
калі
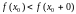 ,
то
не набывае значэнняў з інтэрвала
,
то
не набывае значэнняў з інтэрвала
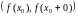 .
У абодвух выпадках мноства значэнняў
функцыі не ёсць адрэзак. ?!? (Калі ж
.
У абодвух выпадках мноства значэнняў
функцыі не ёсць адрэзак. ?!? (Калі ж
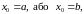 то разглядаецца толькі адпаведны
аднабаковы ліміт.) ■
то разглядаецца толькі адпаведны
аднабаковы ліміт.) ■
