1. Последовательность .

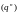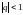Пакажам, што лікавая паслядоўнасць пры – (бмп), а пры ёсць (бвп).

∆ Калі 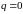, то паслядоўнасць ёсць (бмп) (уласцівасць 4°. Калі лікавая паслядоўнасць 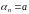ёсць сталая і (бмп), то 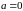.). Няхай 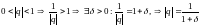. На падставе няроўнасці Бэрнулі ( 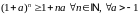  , прычым роўнасць толькі пры ) маем 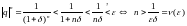г.зн. лікавая паслядоўнасць –(бмп) пры  . На падставе тэарэмы пра сувязь паміж (бмп) і (бвп) атрымліваецца, што – (бвп) пры  .◄

2. Теорема о представлении сходящейся числовой последовательности.

Тэарэма (пра выяўленне збежнай лікавай паслядоўнасці). Для таго каб лікавая паслядоўнасць 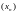мела лімітам лік , неабходна і дастаткова, каб , дзе ёсць бясконца малая паслядоўнасць .

□ (Неабходнасць) Няхай і , то лікавая паслядоўнасць ёсць бясконца малая паслядоўнасць. Гэта азначае, што мае месца выяўленне , дзе 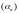– бясконца малая паслядоўнасць.

(Дастатковасць) Няхай , – бясконца малая паслядоўнасць. Паколькі ёсць бясконца малая паслядоўнасць, то лікавая паслядоўнасць 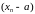таксама (бмп), г.зн. . ■

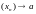3. Предел частного двух сходящихся числовых последовательностей.

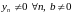(Ліміт дзелі дзвюх збежных лікавых паслядоўнасцяў) Калі і , то .

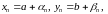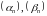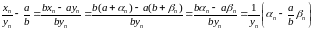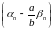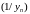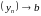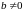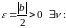
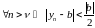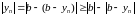
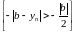
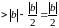□ Маем дзе – бясконца малыя паслядоўнасці. Таму . З уласцівасцяў бясконца малых паслядоўнасцяў вынікае, што ёсць (бмп). Пакажам, што лікавая паслядоўнасць – абмежаваная. Паколькі і , то для . Далей атрымаем , г.зн. , або 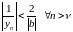, а таму 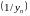– абмежаваная лікавая паслядоўнасць(Чаму?). Такім чынам, 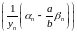– (бмп). Гэта значыць, мае месца выяўленне 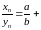(бмп). На падставе тэарэмы пра выяўленне збежнай паслядоўнасці маем . ■

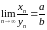4. Предельный переход в неравенствах.

Тэарэма. (пра лімітавы пераход у няроўнасцях). Калі, пачынаючы з некаторага нумара, для элементаў дзвюх збежных лікавых паслядоўнасцяў 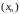і 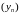праўдзяцца няроўнасці , то ліміты гэтых паслядоўнасцяў праўдзяць няроўнасць .

□ (ад процілеглага) Няхай , але 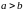. Возьмем лік 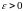настолькі малы, каб праўдзілась няроўнасць 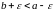. (2)

(Дастаткова ўзяць 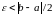.) Паколькі 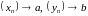, то для выбранага ліку зноўдзецца , што раўназначна няроўнасцям (3)

. (4)

Выкарыстоўваючы па чарзе спачатку правую няроўнасць з (4), затым няроўнасць (2) і, нарэшце, левую няроўнасць з (3), атрымаем 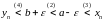, адкуль вынікае, што ■

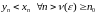5. Теорема о сжатой последовательности.

Тэарэма (пра сціснутую паслядоўнасць, або прынцып двух міліцыянтаў). Калі 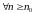мае месца няроўнасць 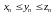(5)

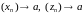і , то і .

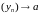□ Выберам адвольна . Паколькі паслядоўнасці 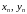– збежныя, то 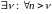праўдзяцца няроўнасці (6)

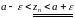. (7)

Беручы адпаведныя няроўнасці з (6), (5) і (7), атрымаем .

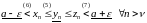З гэтых няроўнасцяў вынікае , г.зн. . ■