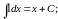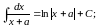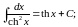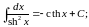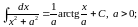- •Определения.
- •Ограниченное множество. Верхняя и нижняя границы множества.
- •Точные верхняя и нижняя границы множества. При помощи математических символов.
- •Неограниченность множества сверху и снизу.
- •Кратный корень многочлена.
- •Неограниченная и бесконечно большая числовая последовательность.
- •Бесконечно малая, сходящаяся, расходящаяся числовая последовательность.
- •Числовой ряд. Сходимость числового ряда.
- •Монотонная числовая последовательность.
- •Последовательности вложенных и стягивающихся отрезков.
- •Подпоследовательность числовой последовательности. Частичный предел.
- •Фундаментальная числовая последовательность.
- •Предел функции в точке и на , бесконечный предел. Односторонние пределы.
- •Непрерывность функции в точке и на множестве.
- •Первая и вторая тэоремы Вейерштрасса.
- •Равномерная непрерывность.
- •Точка разрыва функции. Типы разрывов.
- •Монотонная функция, сложная и обратная функции.
- •Эквивалентные функции. Бесконечно малые функции более высокого порядка.
- •Производная функции, односторонние производные.
- •Геометрический смысл производной.
- •Теоремы Ферма, Ролля, Коши и Лагранжа для дифференцируемых функций.
- •Основные формулы
- •— Непарыўная і перыядычная з перыядам т, то
— Непарыўная і перыядычная з перыядам т, то
Формулы площади криволинйной трапеции и криволинейного сектора.
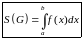
 трапеция
трапеция

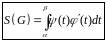 сектор
сектор
Формула вычисления длины кривой.
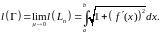
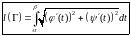

Формулы вычисления объёма тела вращения вокруг обеих координатных осей.
 ох
ох
 оу
оу

Таблицы производных и интегралов.


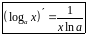








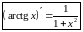





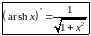



|
|
|
|
|
|
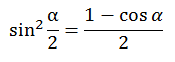
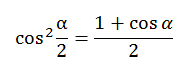
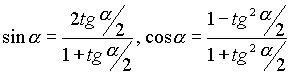
1º Збежная лікавая паслядоўнасць мае толькі адзін ліміт.
2º Збежная лікавая паслядоўнасць ёсць абмежаваная.
3º
Сума
[розніца]
дзвюх
збежных лікавых паслядоўнасцяў
 і
і
 ёсць збежная лікавая паслядоўнасць,
якая мае лімітам суму
[розніцу]
лімітаў
паслядоўнасцяў
і
.
ёсць збежная лікавая паслядоўнасць,
якая мае лімітам суму
[розніцу]
лімітаў
паслядоўнасцяў
і
.
4º Здабытак дзвюх збежных лікавых паслядоўнасцяў і ёсць збежная лікавая паслядоўнасць, якая мае лімітам здабытак лімітаў паслядоўнасцяў і .
5º
(Ліміт
дзелі дзвюх збежных лікавых паслядоўнасцяў.)
Калі
 і
і
 ,
то
,
то
 .
.
Тэарэма
(сувязь
паміж (бмп)
і (бвп)).
Калі
лікавая паслядоўнасць
![]() ёсць (бвп) і
ёсць (бвп) і
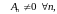 то лікавая паслядоўнасць
то лікавая паслядоўнасць
![]() ёсць (бмп). Калі лікавая паслядоўнасць
ёсць (бмп). Калі лікавая паслядоўнасць
![]() – (бмп) і
– (бмп) і
 то лікавая паслядоўнасць
то лікавая паслядоўнасць
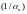 – (бвп).
– (бвп).

Тэарэма(неабходная
ўмова дыферэнцавальнасці). Калі
функцыя
 ёсць дыферэнцавальная ў пункце
,
то яна непарыўная ў гэтым пункце.
ёсць дыферэнцавальная ў пункце
,
то яна непарыўная ў гэтым пункце.