Теоремы Ферма, Ролля, Коши и Лагранжа для дифференцируемых функций.
Тэарэма
Фэрма.
Калі
функцыя
ёсць дыферэнцавальная ў пункце
і мае ў пункце
лакальны экстрэмум, то
.
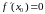Тэарэма
Ролля. Няхай
функцыя
ёсць: 1)
непарыўная на
;
2) дыферэнцавальная
на
;
3)
.
Тады існуе прынамсі адзін пункт
.
Тэарэма Кашы.
Калі
функцыі
і
– непарыўныя на
,
дыферэнцавальныя на
і
,
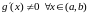то
Тэарэма Лягранжа.
Калі
функцыя
ёсць непарыўная на
,
і дыферэнцавальныя на
,
то
.
Критерий постоянства функций.
Тэарэма (крытэр сталасці дыферэнцавальнай функцыі). Для таго каб дыферэнцавальная на адрэзку функцыя была сталаю, неабходна і дастаткова, каб яе вытворная была роўная нулю на гэтым адрэзку.
Теорема о совпадающих производных.
Тэарэма (пра супаданыя вытворныя). Калі дзве функцыі маюць на інтэрвале супаданыя вытворныя, то яны розняцца адна ад другой на гэтым інтэрвале на канстанту.
Критерий интегрируемости функции на отрезке.
Крытэр
інтэгравальнасці.
Для таго каб функцыя
,
вызначаная і абмежаваная на адрэзку
,
была інтэгравальнаю на гэтым адрэзку,
неабходна і дастаткова, каб гэтая функцыя
адпавядала ўмове
г.зн.
.
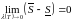Монотонность и аддитивность определённого интеграла.
(манатоннасць інтэграла). Калі функцыі і інтэгравальныя на і , то . (адытыўнасць інтэграла) Калі функцыя інтэгравальная на , то .
Теоремы о среднем значении интегрируемой и непрерывной функций.
(інтэгравальнай
функцыі).
Калі функцыя
ёсць інтэгравальная на адрэзку
,
то існуе лік
,
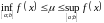такі, што
.
(непарыўнай
функцыі).
Калі
функцыя
ёсць непарыўная, то існуе лік
такі, што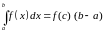
Непрерывность и дифференцируемость интеграла с переменной верхней границей.
Тэарэма (Непарыўнасць
інтэграла са зменнаю верхняю мяжою).
Калі функцыя
ёсць інтэгравальная на
,
то функцыя
ёсць непарыўная на
.
Основные формулы
Формула бинома Ньютона.
Формула вычисления биномиальных коэффициентов.
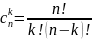
Вычисление корня из комплексного числа.
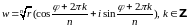
Число
как сумма ряда и как предел числовой
последовательности.
.
Замечательные тригонометрический и степенно-показательный пределы.
Уравнения касательной и нормали к графику функции
Формулы вычисления дифференциалов первого и высших порядков.
=
Формула Лейбница вычисления производной
-го
порядка произведения.
Формула вычисления неопределённого интеграла по частям.
Формула замены переменной в неопределённом интеграле.
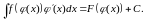
Метод Остроградского вычисления неопределённого интеграла.
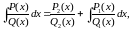
Формула Лагранжа конечных приращений.
Подстановки Эйлера для рационализации интеграла
.
,
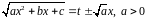або
.
Вычисление интегралов
.
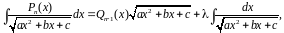
Формулы, выражающие интегралы от чётной, нечётной и периодической фун.
–
цотная:
–
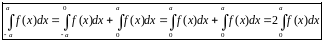
няцотная:
