
- •Определения.
- •Ограниченное множество. Верхняя и нижняя границы множества.
- •Точные верхняя и нижняя границы множества. При помощи математических символов.
- •Неограниченность множества сверху и снизу.
- •Кратный корень многочлена.
- •Неограниченная и бесконечно большая числовая последовательность.
- •Бесконечно малая, сходящаяся, расходящаяся числовая последовательность.
- •Числовой ряд. Сходимость числового ряда.
- •Монотонная числовая последовательность.
- •Последовательности вложенных и стягивающихся отрезков.
- •Подпоследовательность числовой последовательности. Частичный предел.
- •Фундаментальная числовая последовательность.
- •Предел функции в точке и на , бесконечный предел. Односторонние пределы.
- •Непрерывность функции в точке и на множестве.
- •Первая и вторая тэоремы Вейерштрасса.
- •Равномерная непрерывность.
- •Точка разрыва функции. Типы разрывов.
- •Монотонная функция, сложная и обратная функции.
- •Эквивалентные функции. Бесконечно малые функции более высокого порядка.
- •Производная функции, односторонние производные.
- •Геометрический смысл производной.
- •Теоремы Ферма, Ролля, Коши и Лагранжа для дифференцируемых функций.
- •Основные формулы
- •— Непарыўная і перыядычная з перыядам т, то
Монотонная функция, сложная и обратная функции.
Функцыю
 называюць нарастальнай
на
мностве
называюць нарастальнай
на
мностве
 ,
калі
,
калі
 ;
неспадальнай,
калі
;
неспадальнай,
калі
 ;
спадальнай,
калі
;
спадальнай,
калі
 ;
ненарастальнай,
калі
;
ненарастальнай,
калі
 .
Усе такія функцыі называюцца манатоннымі.
Нарастальныя і спадальныя функцыі
называюцца строга
манатоннымі.
.
Усе такія функцыі называюцца манатоннымі.
Нарастальныя і спадальныя функцыі
называюцца строга
манатоннымі.
Няхай
функцыя
 вызначана
на
вызначана
на
 ,
а функцыя
,
а функцыя
 вызначана на
вызначана на
 ,
прычым
,
прычым
 .
Тады функцыю, якая
.
Тады функцыю, якая
 набывае значэнне
набывае значэнне
 ,
называюць складанай
функцыяй
(або
кампазіцыяй,
або суперпазіцыяй)
функцый
,
называюць складанай
функцыяй
(або
кампазіцыяй,
або суперпазіцыяй)
функцый
 і абазначаюць
і абазначаюць
 .
.
Няхай
функцыя
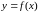 вызначаная на
і строга манатонная на
,
г.зн.
вызначаная на
і строга манатонная на
,
г.зн.
 ,
а тым самым
,
а тым самым
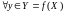 існуе толькі адзін лік
існуе толькі адзін лік
 такі, што
.
Такім чынам на мностве
такі, што
.
Такім чынам на мностве
 вызначана функцыя, якая называецца
адваротнаю
функцыяй
да функцыі
і абазначаецца
вызначана функцыя, якая называецца
адваротнаю
функцыяй
да функцыі
і абазначаецца
 .
Відочна, што
.
Відочна, што
 ,
а
,
а

Эквивалентные функции. Бесконечно малые функции более высокого порядка.
Калі
функцыі
і
 вызначаны ў праколатай акрузе пункта
вызначаны ў праколатай акрузе пункта
 і
і
 ,
то функцыі
,
то функцыі
 называюць эквівалентнымі
ў акрузе пункта
і пішуць
называюць эквівалентнымі
ў акрузе пункта
і пішуць
 .
.
Калі
 і
і
 ,
то кажуць, што функцыя
у акрузе пункта
ёсць
бясконца
малая больш высокага парадку,
чым
.
,
то кажуць, што функцыя
у акрузе пункта
ёсць
бясконца
малая больш высокага парадку,
чым
.
Производная функции, односторонние производные.
Няхай
функцыя
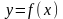 вызначана ў акрузе пункта
вызначана ў акрузе пункта
 .
Калі існуе
.
Калі існуе
 ,
то гэты ліміт называецца вытворнай
функцыі
у пункце
.
,
то гэты ліміт называецца вытворнай
функцыі
у пункце
.
К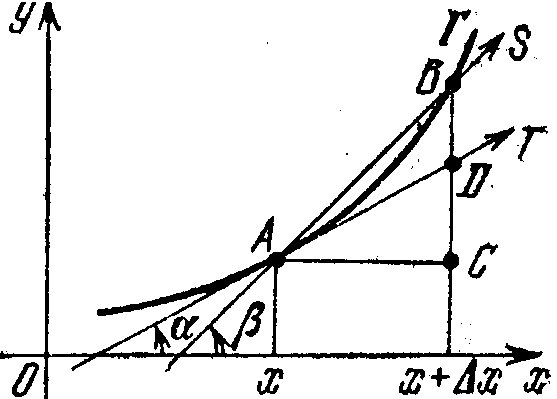 алі
існуюць
алі
існуюць
 і
і
 то іх называюць адпаведна левабаковай
і
правабаковай
вытворнымі
функцыі
то іх называюць адпаведна левабаковай
і
правабаковай
вытворнымі
функцыі
 у пункце
у пункце
 і
абазначаюць адпаведна
і
абазначаюць адпаведна
 і
і
 .
.
Геометрический смысл производной.
П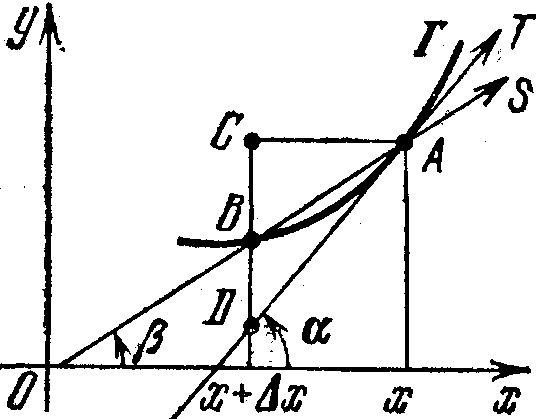 усть
на интервале (а,b)
задана непрерывная функция у=f(x).
Её график наз. непрерывной кривой.
Обозначим его через Г. Зададим на Г точку
А=(х,f(х))
(рис) и поставим целью определить
касательную к Г в этой точке. Для этого
введем на Г другую точку B=(x+x,f(x+x)),
где x0
(рис. 1 изображён случай x>0,
а на рис. 2 – случай x<0).
Прямую, проходящую через точки А и
В, направленную в сторону возрастания
х (отмеченную стрелкой), наз. секущей и
обозначим через S.
Угол, который S
образует с положительным направлением
оси х, обозначим через .
Мы считаем, что –/2<<
/2.
При >0
угол отсчитывается от оси x против
часовой стрелки, а при <0
по часовой стрелке. На данных рисунках
>0.
На рис. 1 x=AC,
y=СВ,
а на рис. 2 x=–AC,
y=–СВ,
В обоих случаях y/x=tg.
усть
на интервале (а,b)
задана непрерывная функция у=f(x).
Её график наз. непрерывной кривой.
Обозначим его через Г. Зададим на Г точку
А=(х,f(х))
(рис) и поставим целью определить
касательную к Г в этой точке. Для этого
введем на Г другую точку B=(x+x,f(x+x)),
где x0
(рис. 1 изображён случай x>0,
а на рис. 2 – случай x<0).
Прямую, проходящую через точки А и
В, направленную в сторону возрастания
х (отмеченную стрелкой), наз. секущей и
обозначим через S.
Угол, который S
образует с положительным направлением
оси х, обозначим через .
Мы считаем, что –/2<<
/2.
При >0
угол отсчитывается от оси x против
часовой стрелки, а при <0
по часовой стрелке. На данных рисунках
>0.
На рис. 1 x=AC,
y=СВ,
а на рис. 2 x=–AC,
y=–СВ,
В обоих случаях y/x=tg.
Если x0, то y0 и точка В, двигаясь по Г, стремится к A. Если при этом угол стремится к некоторому значению , отличному от /2 и –/2, то существует предел limx0y/x=limtg=tg [1], равный производной (конечной) от f в точке x: f'(x)=tg [2]. Обратно, если существует (конечная) производная f'(x), то =arctg f'(x). При стремлении к секущая S стремится занять положение направленной прямой Т, проходящей через точку А и образующей угол с положительным направлением оси х. Направленная прямая Т наз. касательной к кривой Т в её точке А. Определение: Касательной к кривой Г (y=f(x)) в её точке А=(х,f(х)) наз. направленная прямая Т, к которой стремится секущая S (направленная в сторону возрастания х прямая), проходящая через А и точку В=(x+x,f(x+x))Г, когда x>0. Мы доказали, что если непрерывная, функция у=f(х) имеет конечную производную f'(х) в точке х, то её график Г в соответствующей точке имеет касательную с угловым коэффициентом tg=f'(х) (–/2<</2). Обратно, существование предела lim=(–/2<</2)
влечет за собой существование конечной производной f'(х) и справедливость равенств (1), (2). Может случиться, что f имеет в точке х правую и левую производные, отличные между собой: f'(x)f'пр(x).
Т огда
А есть угловая точка Г. В этом случае
касательная к Г в A не существует, но
можно говорить, что существуют правая
и левая касательные с разными угловыми
коэффициентами:
огда
А есть угловая точка Г. В этом случае
касательная к Г в A не существует, но
можно говорить, что существуют правая
и левая касательные с разными угловыми
коэффициентами:
Дифференциал. Инвариантность формы дифференциала.
Галоўную
лінейную частку
 прыросту дыферанцавальнай ў пункце
функцыі
(гл. (1)) называюць дыферэнцыялам
функцыі і абазначаюць
прыросту дыферанцавальнай ў пункце
функцыі
(гл. (1)) называюць дыферэнцыялам
функцыі і абазначаюць
 .Дыферэнцыял
функцыі
мае адзін і той самы выгляд
.Дыферэнцыял
функцыі
мае адзін і той самы выгляд
 не гледзячы на тое, ці ёсць x
незалежная зменная, ці х – дыферэнцавальная
функцыя якой-небудзь іншай зменнай.
Гэтую ўласцівасць дыферэнцыяла называюць
інварыянтавасцю
формы дыферэнцыяла.
не гледзячы на тое, ці ёсць x
незалежная зменная, ці х – дыферэнцавальная
функцыя якой-небудзь іншай зменнай.
Гэтую ўласцівасць дыферэнцыяла называюць
інварыянтавасцю
формы дыферэнцыяла.
Локальный экстремум функции.
Няхай
існуе
 –акруга
пункта
,
–акруга
пункта
,
 ,
ў якой вызначана функцыя
і
,
ў якой вызначана функцыя
і
 .
Тады кажуць, што функцыя
мае ў пункце
лакальны
максімум (мінімум).
Лакальны максімум і лакальны мінімум
аб’ядноўваюць агульным тэрмінам
лакальны
экстрэмум.
.
Тады кажуць, што функцыя
мае ў пункце
лакальны
максімум (мінімум).
Лакальны максімум і лакальны мінімум
аб’ядноўваюць агульным тэрмінам
лакальны
экстрэмум.
Первообразная и неопределённый интеграл.
Дыферэнцавальная
на інтэрвале Х
функцыя
 называецца першаіснаю
для функцыі
на
Х, калі
называецца першаіснаю
для функцыі
на
Х, калі
 .
.
Калі
ёсць першаісная для
на інтэрвале Х
, то сукупнасць
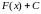 першаісных для
называюць
нявызначаным
інтэгралам
ад функцыі
першаісных для
называюць
нявызначаным
інтэгралам
ад функцыі
 на
Х
і абазначаюць
на
Х
і абазначаюць
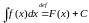 .
.
Интегральная сумма и определённый интеграл для функции
 на отрезке
на отрезке
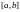 .
.
Суму
 будзем называць інтэгральнаю
сумай для
функцыі
пры зададзеным падзеле
будзем называць інтэгральнаю
сумай для
функцыі
пры зададзеным падзеле
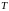 і фіксаванай выбарцы
і фіксаванай выбарцы
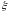 .
.
Лік I
называюць вызначаным
інтэгралам
функцыі
на адрэзку
 і абазначаюць
і абазначаюць
 , калі
, калі
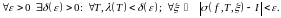
Верхняя и нижняя суммы Дарбу.
Няхай
абмежаваная на
,
і
– некаторы падзел адрэзка
.
Няхай
 .
Сумы
.
Сумы
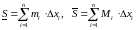 называюцца
адпаведна ніжняй
і верхняй
сумамі Дарбу
для дадзенага падзелу
.
называюцца
адпаведна ніжняй
і верхняй
сумамі Дарбу
для дадзенага падзелу
.
Монотонность и аддитивность определённого интеграла.
(манатоннасць
інтэграла).
Калі
функцыі
![]() і
і
![]() інтэгравальныя на
інтэгравальныя на
![]() і
і
 , то
, то
 .
.
(адытыўнасць інтэграла) Калі функцыя інтэгравальная на , то
 .
.
Интеграл с переменной верхней границей.
Калі
функцыя
ёсць інтэгравальная на
 ,
то
,
то
![]() існуе інтэграл
існуе інтэграл
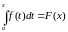 ,
які называюць
інтэгралам
са зменнаю верхняю мяжою.
,
які называюць
інтэгралам
са зменнаю верхняю мяжою.
Формулировки теорем
Теорема о гранях.
Кожнае непустое абмежаванае зверху [ знізу ] мноства рэчаісных лікаў мае дакладную верхнюю [ ніжнюю ] мяжу.
Предельный переход в неравенстве. Теорема о сжатой последовательности.
Тэарэма
(пра
лімітавы пераход у няроўнасцях). Калі,
пачынаючы з некаторага нумара, для
элементаў дзвюх збежных лікавых
паслядоўнасцяў
і
 праўдзяцца няроўнасці
праўдзяцца няроўнасці
![]() ,
то ліміты гэтых паслядоўнасцяў праўдзяць
няроўнасць
,
то ліміты гэтых паслядоўнасцяў праўдзяць
няроўнасць
![]() .
.
Тэарэма
(пра
сціснутую паслядоўнасць, або
прынцып двух міліцыянтаў).
Калі
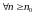 мае месца няроўнасць
мае месца няроўнасць
 і
і
 ,
то і
,
то і
 .
.
Критерий сходимости монотонной последовательности.
Тэарэма (Крытэр збежнасці манатоннай паслядоўнасці). Для таго каб манатонная паслядоўнасць была збежнаю, неабходна і дастаткова, каб яна была абмежаванаю.
Критерий Коши сходимости числовой последовательности.
Тэарэма (Крытэр Кашы збежнасці лікавай паслядоўнасці). Для таго каб лікавая паслядоўнасць была збежнаю, неабходна і дастаткова, каб яна была фундаментальнаю.
Принцип выбора (Теорема Больцано-Вейерштрасса).
Тэарэма (Бальцана-Ваерштраса або прынцып выбару). З кожнай абмежаванай лікавай паслядоўнасці можна вылучыць збежную падпаслядоўнасць.
Критерии Гейне и Коши существования предела функции.
Тэарэма (крытэр
Гайне існавання ліміту функцыі). Для
таго каб функцыя
мела лімітам лік
у пункце
 ,
неабходна і дастаткова, каб для кожнай
лікавай паслядоўнасці
значэнняў аргумента функцыі
,
,
неабходна і дастаткова, каб для кожнай
лікавай паслядоўнасці
значэнняў аргумента функцыі
,
 адпаведная лікавая паслядоўнасць
значэнняў функцыі
адпаведная лікавая паслядоўнасць
значэнняў функцыі
 .
.
Крытэр
Кашы (існавання
ліміту функцыі). Для
існавання ліміту функцыі
у пункце
неабходна і дастаткова, каб
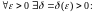

Теорема об односторонних пределах монотонной функции.
Тэарэма (пра
аднабаковыя ліміты манатоннай функцыі).
Калі
функцыя
вызначаная і манатонная на інтэрвале
,
то на гэтым інтэрвале яна можа мець
пункты разрыву толькі першага роду,
г.зн. у кожным пункце
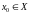 існуюць аднабаковыя ліміты, прычым
існуюць аднабаковыя ліміты, прычым
 (
( ),
калі функцыя
ёсць неспадальная (ненарастальная).
),
калі функцыя
ёсць неспадальная (ненарастальная).
Непрерывность сложной функции.
Калі
функцыя
непарыўная ў пункце
,
прычым
 ,
а функцыя
непарыўная ў пункце
,
а функцыя
непарыўная ў пункце
 ,
то складаная функцыя
,
то складаная функцыя
 непарыўная ў пункце
.
непарыўная ў пункце
.
Теорема о стабилизации знака непрерывной функции.
Калі
функцыя
вызначана ў акрузе пункта
,
непарыўная ў пункце
і
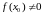 ,
то існуе акруга пункта
,
у якой знак функцыі
супа-дае з яе знакам у пункце
,
г.зн.
,
то існуе акруга пункта
,
у якой знак функцыі
супа-дае з яе знакам у пункце
,
г.зн.

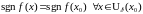 .
.
Теорема о представлении эквивалентных функций.
Тэарэма (Пра
выяўленне эквівалентных функцый). Для
таго каб функцыі f(x)
i
g(x)
былі эквівалентнымі ў акрузе пункта
,
неабходна і дастаткова, каб

Теорема о промежуточном значении непрерывной функции (Теорема Больцано-Коши).
Калі
функцыя f
ёсць непарыўная на адрэзку
і
 ,
то для кожнага рэчаіснага ліку γ , які
размяшчаецца паміж f(a)
і f(b),
існуе прынамсі адзін пункт
,
то для кожнага рэчаіснага ліку γ , які
размяшчаецца паміж f(a)
і f(b),
існуе прынамсі адзін пункт

Первая и вторая теоремы Вейерштрасса для непрерывных функций.
Першая тэарэма Ваерштраса (пра абмежаванасць функцыі). Калі функцыя f ёсць непарыўная на адрэзку , то яна абмежаваная на гэтым адрэзку, г.зн. .
Другая тэарэма Ваерштраса (пра дасягальнасць дакладных межаў). Калі функцыя f непарыўная на адрэзку , то яна дасягае на гэтым адрэзку сваіх дакладных ніжняй і верхняй межаў, г. зн.
.
Теорема Кантора.
Тэарэма Кантара. Калі функцыя ёсць непарыўная на адрэзку, то яна раўнамерна непарыўная на гэтым адрэзку.
Теорема о представлении дифференцируемой функции.
Для
таго, каб функцыя
была дыферанцавальнаю ў пункце
,
неабходна і дастаткова, каб яе прырост
ў гэтым пункце меў выяўленне
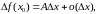 дзе А не залежыць ад
дзе А не залежыць ад
 .
Пры гэтым А=
.
Пры гэтым А= і
і
 ,
або
,
або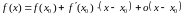 .
.
Теоремы о дифференцировании обратной и сложной функций.
Тэарэма.
Калі строга манатонная і непарыўная на
прамежку Х функцыя
ёсць дыферэнцавальная ў пункце
 і
і
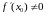 ,
то адваротная функцыя
,
то адваротная функцыя
 ёсць таксама дыферанцавальная ў
адпаведным пункце
ёсць таксама дыферанцавальная ў
адпаведным пункце
 і яе вытворная ёсць
і яе вытворная ёсць
 .
.
Тэарэма
(пра
дыферэнцаванне складанай функцыі).
Калі
функцыя
 ёсць дыферанцавальная ў пункце
,
а функцыя
ёсць дыферанцавальная ў пункце
,
а функцыя
 – дыферэнцавальная ў пункце
,
дзе
– дыферэнцавальная ў пункце
,
дзе
 ,
то складаная функцыя
,
то складаная функцыя
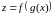 ёсць дыферэнцавальная ў пункце
.
Пры гэтым
ёсць дыферэнцавальная ў пункце
.
Пры гэтым
 .
.
