2. Поновлення одновимірних характеристичних функцій за моментними.

Скористаємось поданням експоненціальної функції 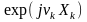степеневим рядом:

.

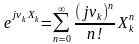Із урахуванням того, що характеристична функція є одновимірною моментною функцією (математичним очікуванням) процесу , а також, що математичне очікування випадкових величин дорівнює сумі їхніх середніх статистичних значень, можна записати:

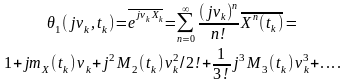(5.7)

Останнє співвідношення і лежить в основі процедури поновлення характеристичних функцій за моментними.

►Приклад. Поновити характеристичну функцію (5.4) за моментними (5.5) та (5.6).

Запишемо по-іншому співвідношення (5.4). Якщо врахувати, що

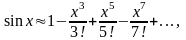а

,

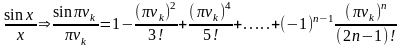то для n=2 дістанемо:

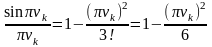. Згідно з (5.4)

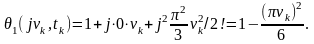
►Приклад. Для процесу з експоненціальним розподілом відповідно до (5.7) та з урахуванням значень математичного очікування та середнього квадрата дістанемо його одновимірну характеристичну функцію

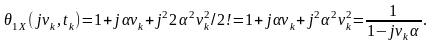
Ураховано відоме з математики співвідношення:

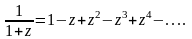
3.Характеристична функція та функція щільності ймовірностей суми незалежних ВП.

Метод характеристичних функцій. Відомо, що для процесу Y(t) характеристична функція 1-го порядку

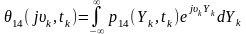
є середньостатистичним експоненти 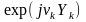. Якщо 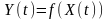, то, незалежно від характеру функціонального зв’язку, відповідно до властивостей середньостатистичного значення

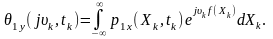
Отже, обчисливши на основі заданих 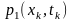та 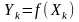одномірну характеристичну функцію 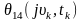та застосувавши до неї зворотне перетворення Фурьє, можна знайти .

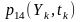Застосування багатомірних характеристичних функцій дозволяє достатньо легко знаходити і багатомірні функції щільності ймовірності.

Приклад.

Розглянемо процес 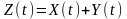, який є сумою двох процесів. Для випадкових величин 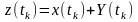в кожному з перерізів (k=1,2,….,n). Будемо вважати та статистично-незалежними величинами. Отже такі величини є некорельованими. Обчислимо характеристичну функцію 1-го порядку процесу Z(t) та функцію щільності ймовірностей 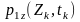.за умови, що закони розподілу складових процесів відомі.

Характеристична функція

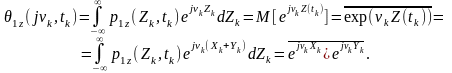
За умови статистичної незалежності, а значить, некорельованості об’єктів середнє значення добутку дорівнює добуткові середніх значень співмножників:

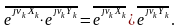
Однак, 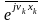= 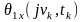, а 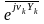= 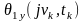.Тому, остаточно:

= .

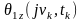• Характеристична функція суми процесів, незалежних (або некорельованих) у співпадаючі моменти часу. є добутком одномірних характеристичних функцій складових процесів.

Функцію щільності ймовірності 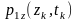тепер можна знайти, обчисливши зворотне перетворення Фур’є від характеристичної функції :

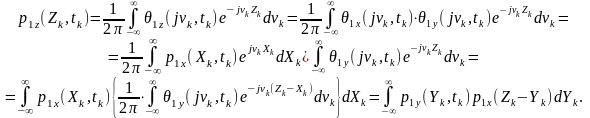
• Одномірна функція щільності ймовірності суми двох незалежних (некорельованих) процесів в співпадаючі моменти часу дорівнює згортці функцій щільності ймовірності складових.

Приклад.

Різниці статистично-незалежних процесів 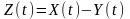:з відомими законами розподілу ймовірності складових відповідає характеристична функція

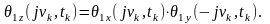
Функція щільності ймовірності

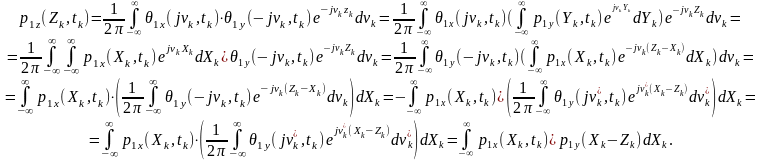
Лекція 6. Кореляційні властивості випадкового процесу.

Статистична незалежність, статистичний зв'язок або кореляція та функціональний зв'язок. Некорельованість та повна кореляція. Кореляційна функція (КФ) як кількісна міра статистичного зв'язку. Автокореляційна функція (АКФ) нецентрованого та центрованого процесів. Зв'язок АКФ з коваріаційною. Фізичний зміст та властивості кореляційної функції процесу.

Література [3, с. 122-154; 9, с. 191-222; 5, с. 161-202].

Завдання на СРС. Кореляційні характеристики статистично незалежних, некорельованих об'єктів та об'єктів з повною кореляцією.