1.Обчислення одновимірних моментних функцій за характеристичними.

Розглянемо одновимірну характеристичну функцію

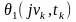
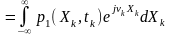(5.1)

та обчислимо за аргументом першу похідну від неї:

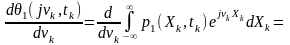
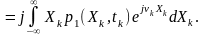
У разі, якщо 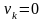, дістанемо:

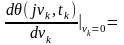
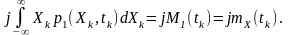
• Початкове значення (для ) похідної першого порядку від одновимірної характеристичної функції з точністю до постійного множника j визначає математичне очікування або одновимірну початкову моментну функцію першого порядку:

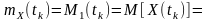
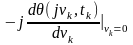(5.2)

Друга похідна від одновимірної характеристичної функції

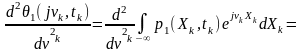
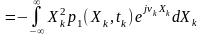
Тоді середній квадрат

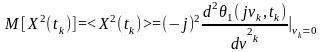(5.3)

• Одновимірна моментна функція другого порядку з точністю до (-j)² пропорційна другій похідній від одновимірної характеристичної функції в точці .

►Приклад. Розглянемо процес Х(t) з експоненціальним законом розподілу

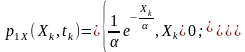
У перерізі t_k математичне очікування такого процесу

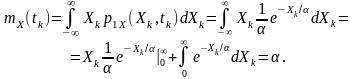
Середній квадрат:

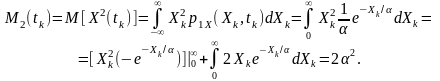
Тоді дисперсія може бути обчислена як різниця між середнім квадратом та квадратом середнього значення:

_.

Обчислимо ці ж величини на основі характеристичної функції першого порядку.

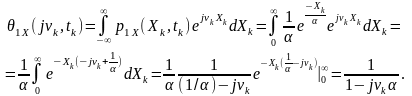
Перша похідна від характеристичної функції

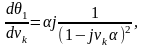
_{а початкове значення похідної}

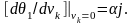
Тоді згідно з (5.2) .

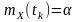Початкове значення другої похідної

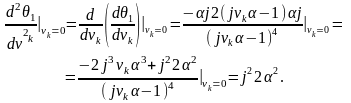
Відповідно до (5.3) середній квадрат

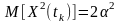
Результати розрахунків із використанням характеристичних функцій повністю збігаються з отриманими раніше на базі визначень математичного очікування та середнього квадрата.

►Приклад. Гармонічне коливання 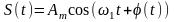визначається випадковую початковою фазою з рівномірним законом розподілу 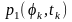на інтервалі 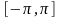і детермінованими амплітудою та частотою. Визначити середнє статистичне, середній квадрат та дисперсію початкової фази методом характеристичних функцій.

Раніше було встановлено, що математичне очікування початкової фази такого процесу 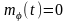, середнє значення квадрата 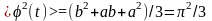, а дисперсія .

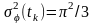Тепер обчислимо такі самі параметри на основі одновимірної характеристичної функції. Для початкової фази заданого гармонічного коливання:

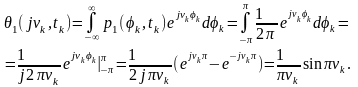_(5.4)

_{Тоді відповідно до (5.2) та з урахуванням останнього співвідношення}

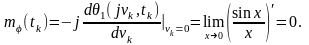_(5.5)

Після двократного диференціювання характеристичної функції та розкриття невизначеності дістанемо середній квадрат та дисперсію:

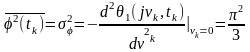. (5.6)

►Приклад. Випадковий процес Х(t) у k-ому перерізі визначається дискретною випадковою величиною Х(t_k)=[1, 2, 3, 4], ймовірності набуття значень якої задаються рядом Р(Х_i)=[0,4; 0,2; 0,1; 0,3]. Визначити середній квадрат та математичне очікування процесу в заданому перерізі методом характеристичних функцій.

Згідно з означенням для дискретної випадкової величини одновимірна характеристична функція

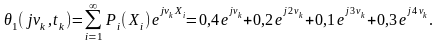
Перша похідна від характеристичної функції за її аргументом

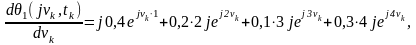
а її початкове значення

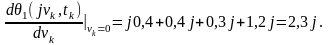
Тоді згідно з (5.2) математичне очікування

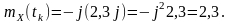
Для визначення середнього квадрата обчислимо початкове значення другої похідної від характеристичної функції:

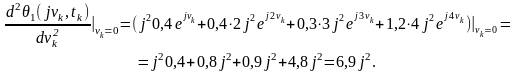Згідно з (7.24) середній квадрат