Процесів із однаковими математичними очікуваннями

та різними дисперсіями.

►Приклад. Дисперсія випадкового процесу з рівномірним законом розподілу.

Відповідно до (4.3) та з урахуванням рівномірного закону розподілу

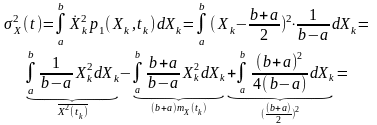(4.5)

►Приклад. Розглянемо незалежне джерело напруги пилкоподібної форми, яке почергово випадково вмикається. Кожному випадковому вмиканню на виході джерела буде відповідати пилкоподібна реалізація, зсунута відносно початку координат вздовж часової осі (рис. 7.7). Установлено, що миттєві значення напруги U(t) в довільному перерізі t_k підпорядковані рівномірному закону розподілу.

Визначити середній квадрат та дисперсію такого процесу.

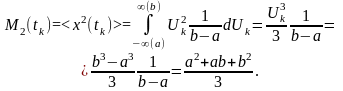(4.6)

Відповідно до (4.4) дисперсія:

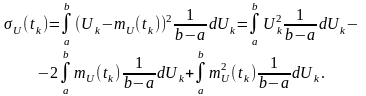
Перша складова в останньому співвідношенні – є середнім квадратом 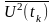, друга - подвоєним значенням квадрата математичного очікування, а третя - квадратом математичного очікування, виходячи з його властивостей.

Тоді

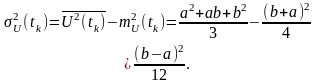(4.7)

Отже,

• дисперсія дорівнює різниці середнього квадрата та квадрата математичного очікування.

Цей висновок за аналогію з детермінованими процесами означає, що потужність змінної складової дорівнює різниці потужностей процесу та його постійної складової.

►Приклад. Випадковий процес Х(t) утворюється гармонічними реалізаціями 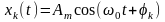, де A_m і постійні величини, а початкова фаза – випадкова величина з рівномірним законом розподілу в інтервалі (рис. 4.4, а). Обчислити математичне очікування та дисперсію випадкової величини та процесу .

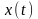У цьому разі миттєві значення процесу є функціями фазового кута. Тому при обчисленні зазначених характеристик для випадкової фази слід виходити з функції щільності ймовірностей фази 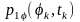, а для випадкового процесу - закону розподілу випадкового процесу .

Обчислимо закон розподілу за . Виділимо інтервал (див рис.4.4,б для однієї реалізації). Тоді ймовірнсть того, що в момент часу миттєві значення реалізацій потраплять в цей інтервал дорівнює .

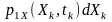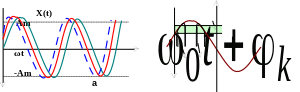
Рисунок 4.4 - Гармонічний процес із рівномірною випадковою

Початковою фазою: а – реалізації випадкового процесу;

б – до визначення закону розподілу.

Оскільки миттєві значення процесу є функціями значень початкової фази 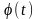і фазового кута 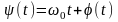, можна стверджувати, що ймовірність визначається ймовірністю потрапляння значень випадкової фази в один із заштрихованих фазових інтервалів. Якщо ймовірність потрапляння випадкової фази в інтервал 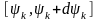позначити через 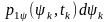, то ймовірність потрапляння в один із двох буде такою:

.

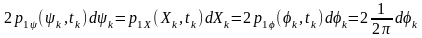Останнє співвідношення випливає з того, що випадкова фаза та початкова випадкова фаза відрізняються невипадковою величиною 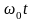, а отже їхні закони розподілу є ідентичними.

Тоді

.

Оскільки

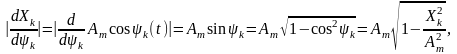
то остаточно,

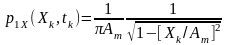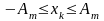, (4.8)

Абсолютне значення похідної введено на тій підставі, що щільність ймовірностей задовольняє умову невід’ємності.

Графік функції зображено на рис 4.5

Математичне очікування випадкової початкової фази

.

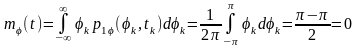Тоді математичне очікування випадкового процесу

.

Оскільки математичне очікування дорівнює нулю, то графік є симетричним відносно початку координат.

Такий самий результат отримаємо, скориставшись визначенням математичного очікування процесу, що є функцією іншого (процес є функцією ) та властивістю інтеграла від парної функції в симетричних межах:

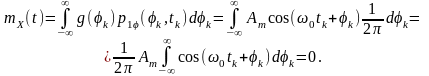
Виходячи з того, що математичне очікування як початкової фази, так і процесу в цілому дорівнює нулю, дисперсії та збігаються із їхніми середніми квадратами: , .

Для рівномірного закону розподілу початкової фази, як відомо,

.

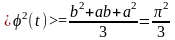Середній квадрат процесу, а отже, і його дисперсія

Корінь квадратний від дисперсії в літературі називається середньоквадратичним відхиленням процесу. В останньому прикладі середньоквадратичне відхилення .

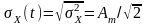С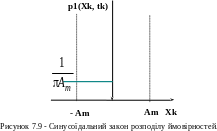 ередньоквадратичне відхилення випадкового процесу, як і центральна моментна функція другого порядку, характеризує флуктуацію миттєвих значень випадкового процесу від середніх, але середньоквадратичне відхилення 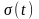має таку ж розмірність, як і процес. Установлено, що по значенню 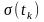можна судити про ширину графіка одновимірної функції щільності ймовірностей .

Як підсумок наведемо характерні властивості дисперсії та середньоквадратичного відхилення:

• дисперсія (середньоквадратичне відхилення) процесу, що не змінюється в часі, дорівнює нулю:

(4.8)

• дисперсія алгебраїчної суми незалежних або некорельованих процесів у моменти часу, що збігаються, є сумою дисперсій її складових:

(4.9)

Підкреслимо, що різниці двох незалежних або некорельованих процесів відповідає сума (не алгебраїчна) їхніх дисперсій;

• дисперсія суми деякого процесу з незмінним у часі процесом дорівнює дисперсії процесу :

. (4.10)

Розглянуті приклади підтверджують зв’язок між одновимірними моментними початковими і центральними функціями першого та другого порядків:

; (4.11)

• якщо два випадкові процеси та в кожному перерізі є корельованими, то дисперсія алгебраїчної суми таких процесів визначається за такою формулою:

, (4.12)

де - взаємна кореляційна функція двох центрованих процесів;

• дисперсія добутку процесу на невипадкову величину (зокрема, число) дорівнює добутку квадрата числа на дисперсію :

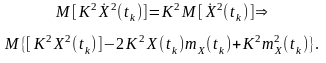(4.13)

Лекція 5. Характеристичні функції та їх зв'язок з моментними функціями.

Обчислення одновимірних моментних функцій 1-го та 2-го порядків по характеристичним функціям. Поновлення характеристичних функцій по моментним. Характеристична функція та функція щільності ймовірностей суми незалежних ВП.

Література [3, с. 80-102; 7, с. 76-89; 10, с. 19-22; 1, 5].