4 Одновимірні моментні функції першого порядку
Початкова одновимірна моментна функція першого порядку (математичне очікування або середньостатистичне значення) визначається усередненням випадкової величини за ансамблем реалізацій процесу будь-якого типу:
=
=
.
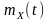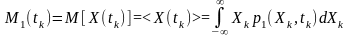(3.4)
Розмірність математичного очікування визначається розмірністю процесу.
Для визначення математичного очікування дискретного процесу застосовують формулу 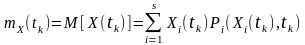(3.5)
,
(3.5)
де
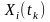- допустимі (точно визначені) значення
випадкової величини
в перерізі
;
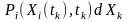- ймовірність того, що дискретна величина
в перерізі
набуває значення, яке збігається з
;
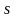– число перерізів, яке в загальному
випадку є нескінченним.
Таким
чином, середнє значення дискретного
випадкового процесу визначається сумою
добутків можливих миттєвих дискретних
значень його реалізацій в одному перерізі
на ймовірності цих значень. Причому
сума може бути як обмеженою (верхній
індекс s
є
величиною кінцевою), так і нескінченною
(верхній індекс
).
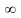Середнє значення дискретної випадкової величини буде зміщуватися в бік тих її значень, які мають більшу ймовірнісну вагу, а за однакових ймовірностей – у бік більших абсолютних значень випадкової величини.
Дослідження підтверджують, що оцінкою математичного очікування є середнє арифметичне отриманих у результаті великої кількості дослідів значень випадкової величини:
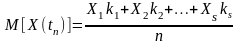
де
–
загальна кількість дослідів;
-
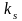кількість дослідів, в результаті яких
спостерігалось значення
.
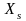С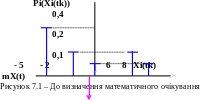
лід
відзначити, що на відміну від випадкового
процесу
математичне очікування є детермінованою
функцією. Ясно, що
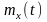для конкретного значення аргумента
є числом. При переході до іншого перерізу
буде змінюватися в загальному випадку
і значення математичного очікування
.
►Приклад.
Випадковий
процес в перерізі
характеризується випадковою дискретною
величиною
=[0,
-2, -5, 6, 8],
ймовірності значень якої задані рядом
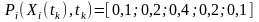
Визначити математичне очікування.
Згідно з (3.5) математичне очікування такого процесу
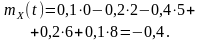
На рис. 3.1 відображені значення випадкової величини, ймовірності кожного з них та математичне очікування. Результат підтверджує факт зміщення (зсуву) значення математичного очікування в бік тих значень випадкової величини, які мають більшу ймовірність.
◙
►Приклад. Визначити математичне очікування процесу X(t), який в перерізі характеризується рівномірним законом розподілу ймовірностей миттєвих значень його реалізацій:
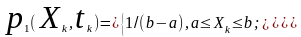(7.6)
Графічне зображення функції щільності ймовірностей для цього закону подано на рис. 3.2.
Площа обмежена графіком цієї функції дорівнює 1, що відповідає умові нормування:
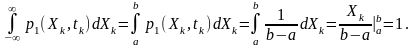
М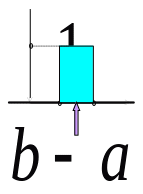
атематичне
очікування
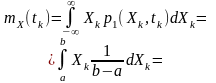(7.7)
◙
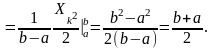
Отже, математичне очікування випадкового процесу з однаковими параметрами рівномірного закону розподілу в кожному перерізі буде однаковим і становить половину суми максимального та мінімального значень, яких набувають вибіркові функції в певному перерізі.
Очевидно, коли абсолютні значення максимального та мінімального значень випадкової величини збігаються, то математичне очікування дорівнює нулю. Це є наслідком більш загального висновку:
математичне очікування випадкової величини з симетричним відносно осі ординат диференціальним законом розподілу ймовірностей дорівнює нулю.
►Приклад.
Визначити
математичне очікування для випадкового
гармонічного процесу, амплітуда якого
є випадковою з рівномірним законом
розподілу в інтервалі
,
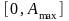а частота
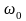та початкова фаза
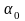являються детермінованими та сталими
(рис.
7.3):
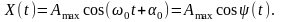
У
перерізі
миттєві значення
процесу
можуть бути в межах від 0 до
.
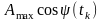Б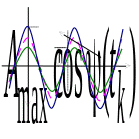
удемо
вважати, що
.
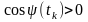Виходячи з того, що амплітуда
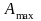є величиною рівномірною, випадкова
величина
буде також задовольняти рівномірному
закону розподілу ймовірностей:
,
.
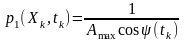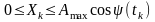Тоді математичне очікування такого процесу
.
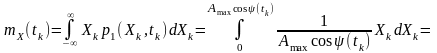
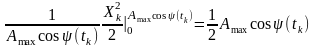Такий самий результат отримаємо, врахувавши, що для рівномірного розподілу
◙
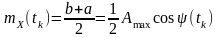
Цей
приклад підтверджує, що математичне
очікування в загальному випадку є
функцією часу
,
навіть якщо закони розподілу в різних
перерізах
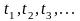збігаються.
Значення випадкового процесу в точці може збігатися або ні з математичним очікуванням, виходячи з імовірнісних характеристик процесу в цьому перерізі.
Ось чому математичне очікування випадкового процесу вважається тим рівнем, що змінюється з часом, рівнем, відносно якого коливаються всі його реалізації (див. рис. 3.4).
Слід зазначити ще і таке: одновимірна початкова функція першого порядку може приймати як додатні, так і від’ємні значення.
Властивості математичного очікування. Перш за все
математичне очікування невипадкового об'єкта
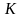є сам об'єкт
:
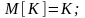
математичне очікування добутку випадкового процесу на невипадкову величину дорівнює добуткові математичного очікування процесу на :
.
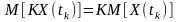
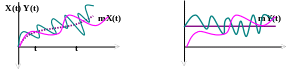Рисунок 3.4 - До визначення математичного очікуваня
процесу.
математичне очікування алгебраїчної суми (добутку) незалежних процесів(закони розподілу однієї випадкової величини не залежать від значень яких набуває інша випадкова величина)визначається алгебраїчною сумою (добутком) математичних очікувань доданків (співмножників):
;
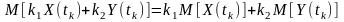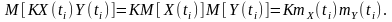
Зауважимо, що математичне очікування алгебраїчної суми процесів дорівнює алгебраїчній сумі їх математичних очікувань і для статистично-залежних або корельованих процесів. Водночас це твердження не є справедливим для операції множення зазначених процесів. Так, якщо процеси є корельованими
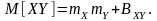
У
останньому співвідношенні складова
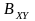відображає кореляційні властивості
двох процесів і називається
взаємною
кореляційною
функцією двох центрованих випадкових
процесів.
І тільки для процесів некорельованих
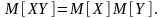
►Приклад.
Випадкові
величини
і
,
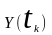що визначають відповідно дискретні
незалежні випадкові процеси чи сигнали
та
,
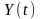характеризуються такими параметрами:
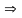
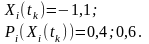
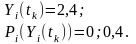
Визначити математичне очікування кожного з процесів та суми процесів у перерізі .
Математичне очікування кожного з процесів:
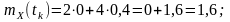
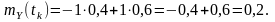
Математичне очікування суми процесів
.
◙
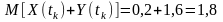Математичне очікування центрованих процесів. Очевидно, що математичне очікування центрованого випадкового процесу або сигналу дорівнює нулю:
.
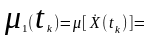
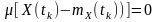Дійсно за означенням
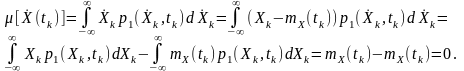
Під
час перетворень останнього виразу
враховано умову нормування для функції
щільності ймовірностей, а також такі
співвідношення:
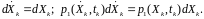
►Приклад.
Визначити
математичне очікування для випадкового
процесу, який в перерізі
характеризується центрованою випадковою
величиною
=[0,4;
-1,6; -4,6; 6,4; 8,4],
ймовірностні
значень якої є такими:
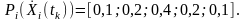
Математичне очікування
◙
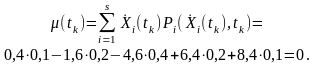Лекція 4. Одновимірна початкова та центральна моментна функція 2-го порядку.
Середній квадрат та дисперсія: визначення, фізичний зміст, особливості для різних типів ВП, розмірність та властивості. Властивості середнього квадрата та дисперсії. Зв'язок з МО. Середній квадрат та дисперсія довільного ВП з рівномірним законом розподілу ймовірностей, гармонічного ВП з рівномірною випадковою фазою. Синусоїдальний закон розподілу. Середньоквадратичне значення
Література [3, с. 80-102; 7, с. 76-89; 10, с. 19-22; 1, 5].