
- •1.Закони розподілу випадкових процесів процесів
- •2. Одновимірні інтегральний та диференціальний закони розподілу
- •Неперервного (а), дискретного (б) та змішаного (в) процесів.
- •Закони розподілу ймовірностей дискретного процесу.
- •Щільності (б) ймовірностей дискретного процесу.
- •1 Загальна характеристика моментних функцій
- •2.Порядок та розмірність момент них функцій
- •3.Початкові моментні функції. Структура формул
- •4 Одновимірні моментні функції першого порядку
- •1.Одновимірні моментні функції другого порядку
- •Очікуваннями і різними дисперсіями.
- •Процесів із однаковими математичними очікуваннями
- •Початковою фазою: а – реалізації випадкового процесу;
- •1.Обчислення одновимірних моментних функцій за характеристичними.
- •2. Поновлення одновимірних характеристичних функцій за моментними.
- •6.1 Види статистичної залежності
- •Кореляцією (б) та некорельовані величини (в).
- •6.2 Двовимірні моментні функції другого порядку
- •7.1 Вкф двох випадкових процесів
- •Його кореляційна функція (б).
- •7.2 Нормовані кореляційні функції.
- •7.3 Особливості кореляційних характеристик
- •1 Визначення стаціонарності у вузькому та широкому значеннях
- •8.2 Математичне очікування,середній квадрат,дисперсія свп
- •8.3 Властивості акф нецентрованого та центрованого свп
- •Процесу (а) та похідної від нього (б).
- •Випадкового процесу.
- •3.Практичне застосування вкф для вирішення проблем виділення слабкого сигналу з суміші.
- •1. Визначення ергодичних випадкових процесів
- •2. Достатні умови ергодичності свп. Умова Слуцького
- •Спектральні характеристики випадкових процесів
- •1. Постановка задачі спектрального аналізу вп
- •2. Енергетичний спектр нестаціонарного вп та його зв'язок з кореляційною функцією.
- •3.Спектральна щільність потужності свп та її фізичний зміст. Спектр флуктуацій (центрованого) свп. Середній квадрат (дисперсія) та спектр свп.
- •4. Властивості спектральної щільності потужності свп. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп
- •5. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп
- •1. Теорема Вінера-Хінчина. Обмеження, що накладаються на акф свп. Додатньо-визначені акф.
- •1.Постановка задачі кореляційного аналізу лінійних систем при дії свп
- •3.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
- •4.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
- •5.Автокореляційна функція реакції. Згортка акф дії та імпульсної характеристики.
- •6. Кореляція процесів на вході та виході лінійної системи. Оцінка статистичного зв'язку "білого шуму" та реакції на нього лінійної системи.
- •З урахуванням властивості дзеркальної симетрії
- •Дійсно,
- •1.Аналіз у частотній області.
- •4. Спектральний аналіз інтегруючої системи при дії "білого шуму".
- •5. Енергетичний спектр реакції ідеального диференціатора.
- •На нього ідеального диференціатора (б).
2.Порядок та розмірність момент них функцій
У
теорії випадкових процесів розрізняють
початкові
та
центральні
моментні
функції, для позначення яких використовують
такі символи:
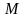 – для початкової моментної функції;
– для початкової моментної функції;
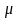 (мю)
– для центральної моментної функції.
(мю)
– для центральної моментної функції.
У
зв’язку з тим, що моментні функції
пов’язані з перерізами, тобто моментами
часу, в які визначені випадкові величини
 ,
їх характеризують розмірністю і виділяють
серед них, подібно законам розподілу
ймовірностей, одновимірні,
двовимірні
та багатовимірні
моментні функції.
,
їх характеризують розмірністю і виділяють
серед них, подібно законам розподілу
ймовірностей, одновимірні,
двовимірні
та багатовимірні
моментні функції.
Моментні функції, як початкові, так і центральні, крім розмірності, характеризуються ще й порядком для чого в позначенні вводиться нижній індекс. Тоді одновимірній моментній функції відповідає однопозиційний індекс, двовимірній – двопозиційний, а -вимірній – -позиційний. У разі дво- та більше позиційного індексу порядок моментної функції визначається сумою чисел кожної позиції.
►Приклад. Визначити розмірність та порядок моментних функцій.
 -
одновимірна початкова моментна функція
порядку
-
одновимірна початкова моментна функція
порядку
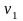 ;
;
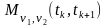 - двовимірна початкова моментна функція
порядку
- двовимірна початкова моментна функція
порядку
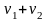 ;
;
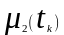 - одновимірна центральна моментна
функція другого порядку;
- одновимірна центральна моментна
функція другого порядку;
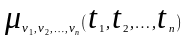 -
-вимірна
центральна моментна функція порядку
-
-вимірна
центральна моментна функція порядку
 .
.
◙
3.Початкові моментні функції. Структура формул
За означенням для випадкового процесу чи сигналу
одновимірна початкова моментна функція порядку
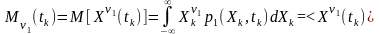 ;
(3.1)
;
(3.1)
двовимірна початкова моментна функція порядку
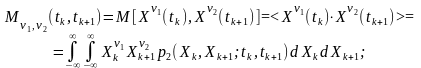 (3.2)
(3.2)
багатовимірна початкова моментна функція
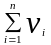 -порядку
-порядку
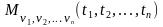 =
= =
=
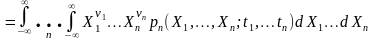 (3.3)
(3.3)
Основні початкові моментні функції:
одновимірна початкова моментна функція першого порядку
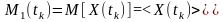 ,
математичне
очікування
або середньостатистичне
значення
випадкового
процесу.
,
математичне
очікування
або середньостатистичне
значення
випадкового
процесу.
Часто
математичне очікування позначають
через
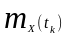 або
або
 .
У загальному випадку для довільного
перерізу індекс
.
У загальному випадку для довільного
перерізу індекс
 можна опустити і тоді середньостатистичне
значення буде мати позначення
можна опустити і тоді середньостатистичне
значення буде мати позначення
 або
або
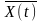 ;
;
одновимірна початкова моментна функція другого порядку
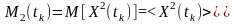 або
середній
квадрат
випадкового процесу. Допускається і
таке позначення:
або
середній
квадрат
випадкового процесу. Допускається і
таке позначення:
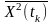 або без індексу
-
або без індексу
-
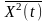 ;
;
двовимірна початкова моментна функція другого порядку
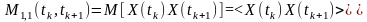 для одного випадкового процесу чи
сигналу, а для двох випадкових процесів
чи сигналів
для одного випадкового процесу чи
сигналу, а для двох випадкових процесів
чи сигналів
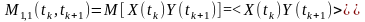 .
Щодо назв використовують найрізноманітніші
варіанти: функція
кореляції процесу
або автокореляційна
функція (АКФ);
функція
взаємної кореляції
двох процесів
.
Щодо назв використовують найрізноманітніші
варіанти: функція
кореляції процесу
або автокореляційна
функція (АКФ);
функція
взаємної кореляції
двох процесів
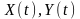 або взаємна
кореляційна
функція (ВКФ).
або взаємна
кореляційна
функція (ВКФ).
Центральні
моментні функції
будь-якого порядку є часовими
характеристиками центрованого
випадкового процесу,
що відрізняється від звичайного
(нецентрованого) на величину його
математичного очікування. Тобто, якщо
– нецентрований випадковий процес,
-
його математичне очікування, то
відповідний центрований випадковий
процес
 .
Зустрічаються і інші назви для центрованого
процесу
.
Зустрічаються і інші назви для центрованого
процесу
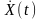 :
відхилення
випадкового процесу від середнього
статистичного або флуктуація
випадкового процесу.
:
відхилення
випадкового процесу від середнього
статистичного або флуктуація
випадкового процесу.
За своєю структурою співвідношення для центральних моментних функцій збігаються з відповідними співвідношеннями, за якими визначають початкові моментні функції нецентрованих випадкових процесів. Так, багатовимірна порядку центральна моментна функція
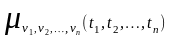 =
=
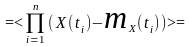

Основні центральні моментні функції:
одновимірна центральна моментна функція другого порядку
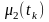 =
=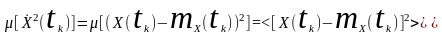 ,
,
яку
називають середньостатистичним
значенням квадрата центрованого
випадкового
процесу або
просто його дисперсією.
Використовують і інші позначення для
дисперсії:
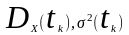 ;
;
двовимірні центральні моментні функції другого порядку:
для центрованого випадкового процесу (його функція кореляції або автокореляційною функція)
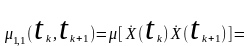
 ;
;
для двох центрованих випадкових процесів
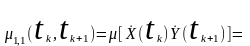
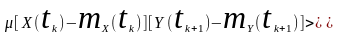 .
.
