1.Аналіз у частотній області.
Під
час опису лінійних систем у частотній
області оперують із комплексною частотною
функцією
,
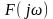яка визначає їхні частотні властивості,
є величиною комплексною та обчислюється
як відношення комплексного миттєвого
значення реакції
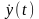до комплексного миттєвого значення
діючого процесу
.
,
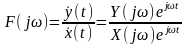де
-
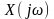та
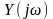– спектральні щільності комплексних
амплітуд відповідно детермінованих
реакції
та дії
,
як пряме перетворення Фур’є від них:
;
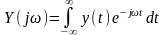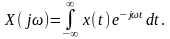
Із теорії лінійних систем відомо, що між комплексною частотною функцією та імпульсною характеристикою має місце взаємно-однозначна відповідність, яка також визначається інтегральним перетворенням Фур'є:
;
.
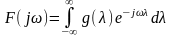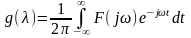Випадкові
процеси в частотній області характеризуються
спектрами потужності дії
та реакції
.
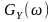Зрозуміло, що визначивши спектр реакції
за заданим спектром діючого на вході
системи процесу
,
зможемо відповідно до теореми
Вінера-Хінчина обчислити і автокореляційну
функцію
(
)
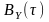реакції,
а отже і інші статистичні характеристики,
зокрема, середній квадрат, дисперсію
та математичне очікування.
Аналіз перетворень випадкових процесів ЛІВ системами у частотній області зводиться до визначення спектральних характеристик реакції за заданими частотними характеристиками системи та спектральними характеристиками діючих процесів.
2. Визначення спектральної щільності потужності реакції лінійної системи на дію СВП
Припустімо, що на вході ЛІВ системи діє випадковий стаціонарний, а значить нескінченно подовжений у часі, сигнал із спектральною щільністю потужності
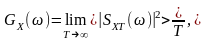
де
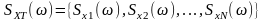- статистичний
ансамбль. Елементом
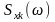такого ансамблю є
модуль спектральної
щільності комплексної амплітуди
відповідної реалізації
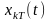випадкового процесу
обмеженої тривалості, який в точності
збігається з процесом
на
інтервалі [-T/2,
T/2
] і
дорівнює нулю за його межами.
Відповідно до спектрального методу аналізу ЛІВ систем модуль спектральної щільності окремої реалізації реакції
.
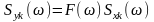Тоді для випадкової стаціонарної реакції спектральна щільність потужності
,
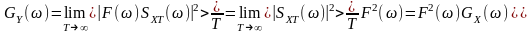де
враховано,
що
квадрат
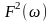модуля комплексної
частотної функції системи не залежить
від Т
і є величиною детермінованою.
Таким чином, спектральна щільність потужності стаціонарної реакції ЛІВ системи на випадкову стаціонарну дію визначається добутком спектральної щільності потужності дії на квадрат модуля комплексної частотної функції системи:
,
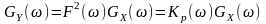де
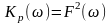- коефіцієнт
передачі потужності.
Для додатних значень частоти, тобто фізичного або одностороннього спектрів:
.
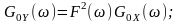
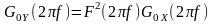За теоремою Вінера-Хінчина визначаємо кореляційну функцію реакції через спектральні характеристики дії та частотні характеристики системи:
.
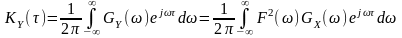3. Спектр реакції та середній квадрат (дисперсія).
Відповідно середній квадрат реакції
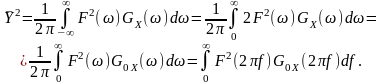
є результатом додавання вкладів від добутку спектра потужності складових діючого процесу та частотного коефіцієнта передачі потужності.
ПІДСУМКИ |
|
1. Аналіз перетворень випадкових процесів ЛІВ системами у частотній області зводиться до визначення спектральних характеристик реакції за заданими частотними характеристиками системи та спектральними характеристиками діючих процесів.
|
2. Спектральна щільність потужності стаціонарної реакції ЛІВ системи на випадкову стаціонарну дію визначається добутком спектральної щільності потужності дії на квадрат модуля комплексної частотної функції системи. 3. Рівність, яка встановлює взаємозв’язок між середнім квадратом стаціонарної реакції ЛІВ системи та спектром потужності дії і коефіцієнтом передачі потужності системи:
|
