Закони розподілу ймовірностей дискретного процесу.
Усі наведені формули для опису законів розподілу справедливі не тільки для неперервних, а і змішаних та дискретних процесів.
Для
дискретних процесів функція розподілу
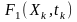записується, як відомо, через функції
Хевісайда. Враховуючи, що
,
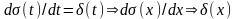для процесів із дискретним характером
функція щільності ймовірностей
.
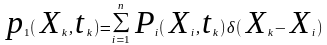(2.12)
Відповідно до (2.12) одновимірний диференціальний закон розподілу такого процесу
.
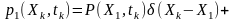
О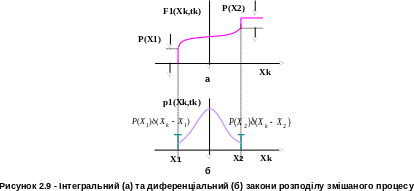
тже,
у разі дискретних процесів функція
щільності ймовірностей
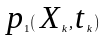є
послідовністю дельта-імпульсів,
зосереджених у точках
,
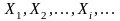із площею кожного, яка дорівнює ймовірності
того, що випадкова величина
набуває
значення відповідно
(рис.2.8,
б).
Поняття дельта-функції використовується при записі диференціального закону і для процесів змішаного типу (дискретно-неперервних). Одновимірна функція розподілу таких процесів поряд з ділянками плавного зростання містить стрибки (рис.2.9, а), висота яких пропорційна ймовірностям набування величиною дискретних значень.
Функція щільності в цих точках набуває нескінченних значень, що відображається дельта-імпульсами з площею відповідної ймовірності (рис.2.9, б).
►Приклад. Знайти функцію щільності ймовірностей процесу Х(t) з функцією розподілу , що зображено на рис. 2.10 а.
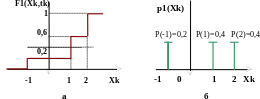
Рисунок 2.10- Приклад функції розподілу (а) та функції
Щільності (б) ймовірностей дискретного процесу.
Математична модель заданої функції розподілу є такою:
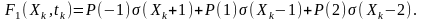
Диференціювання останнього співвідношення дає функцію щільності ймовірностей (див. рис. 2.10б)
.
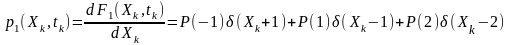Лекція 3. Одновимірна моментна функція 1-го порядку нецентрованих та центрованих процесів.
Порядок та розмірність моментних функцій. Початкові та центральні моментні функції. Структура формул для визначення моментних функцій різної розмірності та порядку. Математичне очікування (МО). Фізичний зміст, розмірність та властивості МО. МО центрованого випадкового процесу (відхилень ВП). МО для дискретних, неперервних та змішаних процесів.
Література [3, с. 80-102; 7, с. 76-89; 10, с. 19-22; 1, 5].
Завдання на СРС. МО довільного процесу та гармонічного процесу з випадковою амплітудою, що задовольняють рівномірному закону розподілу ймовірностей
1 Загальна характеристика моментних функцій
Багатовимірні
закони розподілу ймовірностей є найбільш
повними характеристиками випадкових
процесів. Однак їх практичне застосування
пов’язане
з рядом проблем, розв’язання
яких не завжди можливе. Перш за все
йдеться
про
процеси, закони розподілу ймовірностей
яких невідомі апріорі. З іншого боку,
експериментальне їх виявлення, особливо
для великих значень
,
є дуже трудоємкою та складною процедурою.
Водночас,
хоча і менш детальні, але, зазвичай,
задовільні з практичного погляду
характеристики випадкових процесів,
можна отримати визначенням моментів
випадкових величин
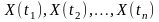на деякому заданому інтервалі T
у відповідних перерізах цих процесів.
Для випадкового процесу такі моменти визначаються як значеннями випадкової величини в конкретному перерізі (миттєвими значеннями реалізацій випадкового процесу), так і значенням часової змінної.
Отже, моменти випадкових процесів є функціями часу, називаються моментними функціями часових аргументів і відносяться до часових характеристик випадкових процесів.
Основу обчислення моментних функцій, як і моментів випадкових величин, складає операція усереднення. Ми вже зустрічались на практиці з такою операцією під час визначення середніх значень детермінованих процесів як функцій часу, зокрема,
- постійної складової періодичного процесу
;
- середньої потужності процесу
.
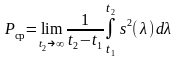Операція усереднення окремої випадкової величини , як сукупності миттєвих значень всіх реалізацій процесу в перерізі , називається усередненням по ансамблю або статистичним усередненням.